Basi 2 - L9 Apr

Introduzione

La logia del primo ordine è una famiglia di linguaggi formali utilizzati per rappresentare informazioni e derivare conseguenze. Ogni logica (come ogni altro linguaggio formale) è definita da una sintassi e una semantica:

Sintassi

Considera il linguaggio come l’insieme delle sequenze finite di simboli ammesse dal linguaggio (formule), dove ogni simbolo appartiene ad un insieme prefissato (alfabeto). La sintassi definisce quindi la struttura delle formule.

Esempio: x+2 ≥ y è una formula ma x2+y ≥ non lo è

Per definire la sintassi di una logica occorre stabilire:

• Quali simboli appartengono al suo alfabeto

• Quali sequenze finite di elementi dell’alfabeto (formule) compongono il linguaggio.

Nota: La sintassi stabilisce quali sequenze di simboli siano formule logiche, e non dice nulla sul loro significato.

Semantica

Definisce il significato di ogni formula della logica, ovvero la sua verità nei diversi mondi possibili. In ogni mondo possibile, una formula può essere “vera” o “falsa”.

Esempio:

• x+2 ≥ y è vero se il valore di x+2 non è minore del valore di y
• x+2 ≥ y è falso in un mondo dove x=0 e y=6

Si dà significato (interpretazione) alle formule più semplici, quelle atomiche ovvero che non possono essere ridotte ulteriormente e poi usando le regole della logica si stabilisce un significato alla altre formule.

Mondo

Dato mondo m e formula $\phi :m|=\phi$ se $\phi$ è vera nel mondo $m⟹m$ modello di $\phi$.

Alfabeto

Semantica

Alfabeto

Linguaggio dei Termini

L’insieme dei termini è definito induttivamente come segue:

• ogni variabile in $V$ è un termine
• ogni simbolo di costante in $F$ è un termine
• se $f$ è un simbolo di funzione ($f\in F$) di arità n > 0 e $t_1,\dots ,t_n$ sono termini, allora anche $f(t_1,\dots ,t_n)$ è un termine.

Linguaggio delle Formule

L’insieme delle formule è definito induttivamente come segue:

• se $p$ è un simbolo di predicato di arità n e $t_1,...,t_n$ sono termini $p(t_1,...,t_n)$ è una formula (detta formula atomica)
• se $\varphi$ e $\psi$ sono formule, lo sono anche:

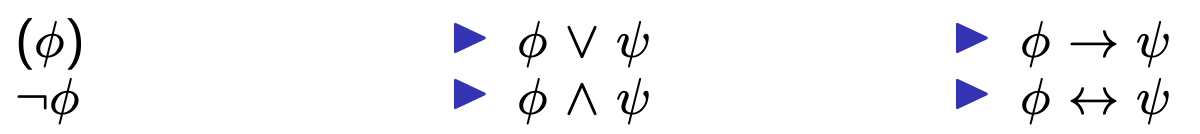
se $\varphi$ è una formula e $X$ è una variabile allora anche $\forall X\varphi$ e $\exists X\varphi$ sono formule.

Scriveremo X = Y invece di $=(X,Y)$ e $X\ne Y$ al posto di$\neg (X=Y)$ (a sua volta al posto di $\neg =(X,Y)$).

Tip

Per capire se una formula è veramente una formula dobiamo poterla divideire in quantificatore, variabile, formula

Interpretazione

Valutazione

Valutazione dei Termini

Valutazione delle Formule