Basi di Dati - Preparazione Orale

Cosa viene Chiesto

Per Algebra Relazionale tutto tranne:

• dimostrazione di correttezza dell’algoritmo per il calcolo della chiusura di X rispetto a G (dove G è l’insieme di dipendenze che risulta da una decomposizione) quindi NON si dimostra la parte la parte X+ rispetto a G contenuto in Z finale
• non si dimostrano le proprietà di mρ(r) ma bisogna AVER CAPITO la sua relazione con r
• parte se della dimostrazione di correttezza dell’algoritmo che verifica il join senza perdita, quindi non si dimostra che se la tabella finale ha una riga di tutte allora il join è senza perdita
• dimostrazione della parte aggiunta all’algoritmo di decomposizione, quindi non si dimostra che aggiungendo uno schema con una chiave si ottiene un join senza perdita

Per l’organizzazione fisica occorre dimostrare di aver compreso le caratteristiche delle varie strutture ed essere in grado di dimostrare i costi delle operazioni.

Per la teoria della concorrenza si dimostra SOLO il teorema del protocollo a 2 fasi, e la correttezza delle regole del timestamp (anche se non c’è un teorema)

OVVIAMENTE non ci sono solo i teoremi, ma anche le definizioni e  occorre dimostrare di aver capito i concetti di base … in pratica i concetti che trovate su slide e dispense TRA i teoremi

Algebra Relazionale

Def 0: Obbiettivo della 3NF 🟢

La Terza Forma Normale (3FN) è una regola di normalizzazione dei database relazionali che mira a eliminare ridondanze e anomalie:

• Anomalia di inserimento: si verifica quando si tenta di inserire un nuovo record e si rischia di creare inconsistenze tra i dati esistenti.
• Anomalia di cancellazione: si verifica quando si tenta di cancellare un record e si rischia di creare inconsistenze tra i dati esistenti.
• Anomalia di aggiornamento: si verifica quando si tenta di aggiornare un dato e si rischia di creare inconsistenze tra le diverse copie del dato.

Queste avvengono quando:

• Più concetti: un unica relazione è utilizzata per rappresentare più concetti
• Ridondanza: si verifica quando lo stesso dato è memorizzato più volte in diverse parti del database.

Def 1: Dipendenza Funzionale 🟢

Dato uno schema relazionale R, una dipendenza funzionale su R è una coppia ordinata di sottoinsiemi non vuoti X e Y di R.

Denominata attraverso $X\to Y$, dove:

• X è il determinante
• Y è il determinato

Def 1.1: Dipendenza Funzionale Banale 🟢

Una dipendenza funzionale $X\to Y$ è detta banale se Y è un sottoinsieme di X.

• $AB\to A$ è banale perché $\{A\}\subseteq \{A,B\}$
• $C\to C$ è banale $\{C\}\subseteq \{C\}$
• $AB\to AB$ è banale $\{A,B\}\subseteq \{A,B\}$

Def 1.2: Soddisfare Dipendenza Funzionale 🟢

Si dice che un’istanza r di R soddisfa la dipendenza funzionale $X\to Y$ se per ogni coppia di tuple t1 e t2 abbiamo che:

Se $t_1[X]=t_2[X]$ allora $t_1[Y]=t_2[Y]$

oss: un’istanza di R è un una tabella che rappresenta le relazione.

Def 1.3: Istanza Legale 🟢

Dati uno schema relazionale R e un insieme di dipendenze funzionali F.

Un’istanza r di R si dice legale se soddisfa tutte le dipendenze funzionali in F.

Def 1.4: Chiusura F+ 🟢

Dato uno schema relazionale R e un insieme di dipendenze funzionali F su R.

La chiusura di F è denotata con $F^{+}$ ed indica l’insieme di dipendenze funzionali che sono soddisfatte da ogni istanza legale di R.

oss: $F\subseteq F^{+}$ ($F$ è contenuto da $F^{+}$)

Def 2: Chiave 🟢

Dati un schema relazionale R ed un insieme di dipendenze funzionali F su R.

Un sottoinsieme K di R si dice chiave se:

• $K\to R\in F^{+}$

• Per ogni sottoinsieme proprio K' di K si ha che $K^{\prime }\to R\notin F^{+}$

Def 3: Attributo Primo e Super-chiave 🟢

Dati uno schema relazionale R e un insieme di dipendenze funzionali F.

• Un attributo A di R si dice primo se appartiene ad una chiave di R.
• Un sottoinsieme X di R si dice super-chiave se contiene una chiave di R o alternativamente determina tutto R (ovvero la sua chiusura è uguale ad R)

Def 4: Dipendenze Parziali e Transitive 🟢

Siano R uno schema relazionale e F un insieme di dipendenze funzionali e una dipendenza $X\to A\in F^{+}$ con $A\notin X$.

La dipendenza si dice parziale se contemporaneamente:

• A non è primo
• X è contenuto propriamente da una chiave ($X\subset K$ contenuto ma diverso)

oss: se non ci sono dipendenze parziali allora gli attributi che non fanno parte di una chiave sono determinati direttamente dalle chiavi.

La dipendenza si dice transitiva se contemporaneamente:

• A non è primo
• per ogni chiave K si ha che X non è contenuto interamente in K e a sua volta X non contiene K, ovvero:
• $X\not\subset K$
• e $K-X\ne \varnothing$ (X non contiene nessuna chiave)

oss: non abbiamo dipendenze transitive se gli attributi che non appartengono alla chiave dipendono direttamente dalla chiave e non da altri attributi non chiave.

Vedi: Dipendenze Parziali e Transitive per esempi

Def 5: Schema in 3NF 🟢

Sia R uno schema relazionale e F un insieme di dipendenze funzionali su R.

R è in 3NF se per ogni dipendenza funzionale $X\to A\in F^{+}$ tale che $A\notin X$ si ha che:

• X è una superchiave, oppure

• A è primo

oss: non vanno controllate le dipendenze funzionali banali ovvero ($X\to At.c.A\notin X$)

Teo 1: 3NF = no parziali e no transitive 🟢

Sia R uno schema relazionale e F un insieme di dipendenze funzionali su R. Lo schema R è 3NF (terza forma normale) se e solo se non esistono dipendenze parziali o transitive.

Obbiettivo dimostrare $3NF⟺\text{no parziali e no transitive}$

Dimostrazione pare SE: ($3NF⟹\text{no parziali e no transitive}$)

Se lo schema è in 3NF allora per ogni dipendenza $X\to A$ abbiamo che $A$ è primo, oppure $X$ è super chiave:

1. Se A è primo viene a mancare la condizione per avere dipendenze parziali e transitive
2. Se A non è primo allora X è superchiave, infatti:

• non possiamo avere dipendenze parziali in quanto la X di quest’ultime deve essere contenuta da una chiave.
• non possiamo avere dipendenze transitive in quanto la X di quest’ultime non deve contenere alcuna chiave.

Dimostrazione parte SOLO SE: ($\text{no parziali e no transitive}⟹3NF$)

Se non abbiamo dipendenze parziali o transitive implica che per ogni dipendenza si ha che:

• A è primo, oppure
• X superchiave, condizione che falsifica sia:
• parziale, infatti se X superchiave allora X non è sotto insieme proprio di K
• transitiva, infatti se X superchiave allora k - X è uguale a $\varnothing$

Quindi è in 3NF.

Chiusura $F^A$ 🟢

Denotiamo con $F^A$ l’insieme di dipendenze funzionali definito nel modo seguente:

• $\text{se}f\in F\text{ allora }f\in F^A$
• Assioma della Riflessività: $\text{se}Y\subseteq X\subseteq R\text{ allora }X\to Y\in F^A$
• Assioma dell’ Aumento: $\text{se}X\to Y\in F^A\text{ allora }XZ\to YZ\in F^A\forall Z\subseteq R$
• Assioma della Transitività: $\text{se}X\to Y\in F^A\text{ e }Y\to Z\in F^A\text{ allora }X\to Z\in F^A$

Gli ultimi tre sono detti assiomi di Armstrong, esistono altre 3 regole che possono essere derivate dagli assiomi di Armstrong che sono utili per determinare da dipendenze di $F^A$ altre dipendenze di $F^A$:

• Regola dell’ Unione: Se $X\to Y\in F^A$ e $X\to Z\in F^A$ allora $X\to YZ\in F^A$
• Regola della Decomposizione: Se $X\to Y\in F^A$ e $Z\subseteq Y$ allora $X\to Z\in F^A$
• Regola della Pseudo-Transitività: Se $X\to Y\in F^A$ e $WY\to Z\in F^A$ allora $WX\to Z\in F^A$

oss: L’insieme $F^A$ può essere ottenuto applicando ricorsivamente gli assiomi di Armstrong su l’insieme di dipendenze funzionali $F$.

Teo 2: Regole derivate da Armstrong 🟢

Sia $F$ un insieme di dipendenze funzionali, allora su questo valgono le 3 regole viste precedentemente:

Dimostrazione:

Unione:

• Se $X\to Y\in F^A$ allora per l’aumento si ha che $X\to XY\in F^A$.
• Analogamente se $X\to Z\in F^A$ sempre per aumento si ha che $XY\to YZ\in F^A$
• Quindi dato che abbiamo $X\to XY$; $XY\to YZ\in F^A$ per transitività possiamo dire che $X\to YZ\in F^A$.

Decomposizione:

• Se $Z\subseteq Y$ allora per riflessività si ha che $Y\to Z\in F^A$ 
• Quindi poiché $X\to Y\in F^A$ e $Y\to Z\in F^A$ per transitività abbiamo che $X\to Z\in F^A$.

Pseudo-Transitività:

• Se $X\to Y\in F^A$, per l’aumento possiamo dire che $WX\to WY\in F^A$ 

• Quindi poiché $WX\to WY\in F^A$ e $WY\to Z\in F^A$ per transitività abbiamo che $WX\to Z\in F^A$.

oss: le tre regole sono:

• Regola dell’ Unione: Se $X\to Y\in F^A$ e $X\to Z\in F^A$ allora $X\to YZ\in F^A$
• Regola della Decomposizione: Se $X\to Y\in F^A$ e $Z\subseteq Y$ allora $X\to Z\in F^A$
• Regola della Pseudo-Transitività: Se $X\to Y\in F^A$ e $WY\to Z\in F^A$ allora $WX\to Z\in F^A$

Def 6: $X^{+}$ 🟢

Siano R uno schema relazionale e F un insieme di dipendenze funzionali su R.

Dato un sottoinsieme di R chiamato X. Denominiamo con $X_F^{+}$ la chiusura di X rispetto a F, dove:

$$X_F^{+}=\{A:X\to A\in F^A\}$$

Ovvero l’insieme degli attributi determinati da X.

Lemma 1 🟢

Siano R uno schema relazionale e F un insieme di dipendenze funzionali su R.

Si ha che $X\to Y\in F^A$ se e solo se $Y\subseteq X^{+}$

Dobbiamo dimostrare che $X\to Y\in F^A⟺Y\subseteq X^{+}$.

Sia $Y=A_1{A}_2\dots A_n$ e $i=0,\dots ,n$

Parte Se ($X\to Y\in F^A⟹Y\subseteq X^{+}$)

Partendo da $X\to Y\in F^A$:

• per decomposizione abbiamo che per ogni i $X\to A_i\in F^A$
• dato che ogni $A_i\in X^{+}$, allora per unione unione quindi $Y\subseteq X^{+}$.

Parte Solo Se ($Y\subseteq X^{+}⟹X\to Y\in F^A$)

Partendo da $Y\subseteq X^{+}$:

• per ogni i si ha che $X\to A_i\in F^A$
• pertanto per unione $X\to Y\in F^A$.

Teo 3: $F^{+}=F^A$ 🟢

Siano R uno schema di relazione ed F un insieme di dipendenze funzionali su R. Si ha $F^{+}=F^A$.

Per dimostrare $F^{+}=F^A$ dobbiamo dimostrare che $F^A\subseteq F^{+}$ e che $F^{+}\subseteq F^A$.

---

Dimostrazione: $F^A\subseteq F^{+}$

Per calcolare $F^A$ si applicano ricorsivamente gli assiomi di Armstrong, dobbiamo dimostrare che ogni dipendenza funzionale ottenuta applichiamo un assioma di Armstrong sia presente anche in $F^{+}$.

Questo può essere fatto per induzione, dove:

• i è il numero di applicazioni di uno degli assiomi di Armstrong.

• il caso base $i=0$ indica che non abbiamo applicato nessun assioma e che quindi $F^A$ contiene soltanto gli elementi in $F$ e banalmente anche $F^{+}$ contiene gli elementi in $F$

• l’Ipotesi induttiva indica che ogni dipendenza funzionale ottenuta a partire da $F$ applicando gli assiomi di Armstrong un numero di volte minore o uguale a i–1 è in $F^{+}$. Tre casi si possono presentare:

1. $X\to Y$ ottenuta attraverso l’assioma della riflessività in tal caso $Y\subseteq X$.

Quindi date due tuple t1 e t2 tali che t1[X] = t2[X], banalmente si ha t1[Y] = t2[Y].

2. $X\to Y$ ottenuta applicando l’assioma dell’aumento ad una dipendenza $V\to W\in F^A$, dove quindi $X=VZ$ e $Y=WZ$ per qualche $Z\subseteq R$ (quindi $X\to Y$ equivale a $VZ\to WZ$).

Sia r un’istanza di R e siano t1 e t2 due tuple in rtali che t1​[X] = t2​[X] (ovvero t1[VZ] = t2[VZ]) si avrà che t1[V] = t2[V] e t1[Z] = t2[Z].

Visto che per ipotesi induttiva $V\to W\in F^{+}$ allora possiamo dire che t1[V] = t2[V] porta ad avere t1[W] = t2[W]. Quindi otteniamo che t1[Y] = T2[Y] (ovvero t1[VZ] = t2[WZ]).

3. $X\to Y$ ottenuta applicando l’assioma della transitività su due dipendenze $X\to Z$ e $Z\to Y$ appartenenti a $F^A$:

Sia r un’istanza di R e siano t1 e t2 due tuple in rtali che t1​[X] = t2​[X].

Per ipotesi induttiva le dipendenze $X\to Z$ e $Z\to Y$ fanno parte di $F^{+}$.

Grazie all’ipotesi induttiva si ha che t1​[X] = t2​[X] $⟹$ t1​[Z] = t2​[Z] e che t1​[Z] = t2​[Z] $⟹$ t1​[Y] = t2​[Y].

Quindi per transitività $X\to Y\in F^{+}$.

---

Dimostrazione: $F^{+}\subseteq F^A$

Il nostro obbiettivo è dimostrare che ogni dipendenza funzionale $X\to Y\in F^{+}⟹X\to Y\in F^A$

Questa dimostrazione è divisa in due sezioni:

La prima parte consiste nel dimostrare che esiste presa $X\to A\in F^{+}$ esiste un’istanza legale di $R$ di questo tipo:

Sia r un’istanza legale e supponiamo per assurdo che la dipendenza funzionale $V\to W\in F$ non sia soddisfatta.

Questo implica che tutti le dipendenze in $F$ hanno uguali valori in V ed hanno diversi valori in W, ovvero che $V\subseteq X^{+}$ e $W\cap (R-X^{+})\ne \varnothing$.

Poiché $V\subseteq X^{+}$, per il Lemma 1 otteniamo che $X\to V\in F^A$, e visto che $V\to W$ allora attraverso l’assioma della transitività possiamo dire che $X\to W\in F^A$.

Se applichiamo il Lemma 1 su $X\to W\in F^A$ otteniamo che $W\subseteq X^{+}$ che contraddice $W\cap (R-X^{+})\ne \varnothing$ dimostrando che non esistono dipendenze funzionali non soddisfatte da r.

La seconda parte consiste nel dimostrare che se $X\to Y\in F^{+}⟹X\to Y\in F^A$.

Sappiamo che $X\to Y\in F^{+}$

Abbiamo mostrato che r è un’istanza legale che quindi soddisfa tutte le dipendenze di $F^{+}$, compresa $X\to Y$.

Poiché $X\subseteq X^{+}$ le due tuple di r coincidono su gli attributi X

Poiché r soddisfa $X\to Y$, allora le due tuple devono coincidere anche sugli attributi di Y.

Questo implica che $Y\subseteq X^{+}$ e, per il Lemma 1 otteniamo che $X\to Y\in F^A$

Algo 1 (calcolo X+) 🟢

Prende come input uno schema R, un insieme F di dipendenze su R e un sottoinsieme X di R. Come output fornisce la chiusura di X rispetto ad F all’interno della variabile Z.

Spiegazione:

Teo 4: Dimostrazione Algo 1 🟢

L’algoritmo 1 calcola correttamente la chiusura di un insieme di attributi $X$ rispetto ad un insieme di dipendenze funzionali $F$.

Dimostrazione:

Indichiamo con $Z^0$ il valore iniziale di $Z$ (ovvero $Z^0=X$) e con $Z^i$ ed $S^i$, i valori di $Z$ e $S$ alla i-esima iterazione.

oss: $Z^i\subseteq Z^{i+1}$ per ogni $i$.

L’obbiettivo è dimostrare che esiste una $i$ tale che $A\in Z^i$ se e solo se $A\in X^{+}$, per fare ciò scomponiamo la dimostrazione in due parti:

• Dimostrazione di $A\in Z^i⟹A\in X^{+}$
• Dimostrazione di $A\in X^{+}⟹A\in Z^i$

---

Parte: $A\in Z^{\text{i}}⟹A\in X^{+}$

L’obiettivo è dimostrare per induzione su i che $Z^{\text{i}}\subseteq X^{+}$ per ogni i, quindi:

Ipotesi Induttiva: $Z^i\subseteq X^{+}$ per ogni i.

Base dell’induzione: la base è i = 0, poiché $Z^{(0)}=X$ e $X\subseteq X^{+}$, si ha che $Z^{(0)}\subseteq X^{+}$

Induzione:

Per ipotesi induttiva $Z^{(\text{i}-1)}\subseteq X^{+}$

Sia A un attributo in $Z^{(\text{i})}-Z^{\text{i}-1}$ (ovvero un attributo aggiunto all’iterazione i)

Deve esistere una dipendenza $Y\to V\in F$ tale che $Y\subseteq Z^{(\text{i}-1)}$ e $A\in V$.

Per il lemma 1 abbiamo che $X\to Y\in F^A$ (visto che $Y\subseteq Z^{(\text{i}-1)}\subseteq X^{+}$)

Poiché $X\to Y\in F^A$ e $Y\to V\in F^A$, per transitività abbiamo che $X\to V\in F^A$, quindi per il lemma 1 $V\subseteq X^{+}$.

Visto che $A\in V$ e $V\subseteq X^{+}$, allora per ogni $A\in Z^{\text{i}}-Z^{\text{i}-1}$ si ha che $A\in X^{+}$, e quindi si conferma l’ipotesi induttiva $Z^i\subseteq X^{+}$

---

Parte: $A\in X^{+}⟹A\in Z^i$

Siano:

• A un elemento di $X^{+}$
• j tale che $S^{(j)}=Z^{(j)}$, ovvero $Z^{(j)}$ è il valore di Z quando l’algoritmo termina

L’obbiettivo è dimostrare che $A\in Z^{(j)}$

Dimostrazione:

• Poiché $A\in X^{+}$, si ha $X\to A\in F^{+}$ (per lemma1 + $F^{+}=F^A$)
• Pertanto $X\to A$ deve essere soddisfatta da ogni istanza legale di R.

Si consideri la seguente istanza r di R, creata basandoci su $X\to A$:

Mostriamo che r è un’istanza legale. Infatti, se, per assurdo, esistesse in F una dipendenza funzionale $V\to W$ non soddisfatta da r, si dovrebbe avere $V\subseteq Z^{(j)}$ e $W\cap (R-Z^{(j)})\ne \varnothing$. Ma si avrebbe che $S^{(j)}\not\subset Z^{(j)}$ (contraddizione).

Quindi r è un istanza legale.

Poiché r è un’istanza legale di R deve soddisfare $X\to A$ che si trova in $F^A$ (e anche $F^{+}$ per il teorema 3) ma, allora, poiché $X=Z^{(0)}\subseteq Z^{(j)}$, A deve essere in $Z^{(j)}$.

Def 7: Decomposizione 🟢

Sia R uno schema di relazione. Una decomposizione di R è una famiglia $\rho =\{R_1,R_2,\dots ,R_k\}$ di sottoinsiemi di R che ricopre R, ovvero tale che ${\bigcup }_{i=1}^k{R}_i=R$.

Def 8: Equivalenza tra insiemi di dipendenze funzionali 🟢

Siano $F$ e $G$ due insiemi di dipendenze funzionali. $F$ e $G$ si dicono equivalenti ($F\equiv G$) se $F^{+}=G^{+}$.

oss: verificare l’equivalenza richiederebbe tempo esponenziale dato che dovremmo calcolare che $F^{+}$ e anche $G^{+}$, per questo possiamo utilizzare il Lemma 2.

Lemma 2 🟢

Siano $F$ e $G$ due insiemi di dipendenze funzionali, se $F\subseteq G^{+}$ allora $F^{+}\subseteq G^{+}$.

Dimostrazione: Sia $f\in F^{+}-F$, poiché per il teorema 3 f è derivabile da F mediante gli assiomi di Armstrong e ogni dipendenza funzionale in F è derivabile da G mediante gli assiomi di armstrong, f è derivabile da G mediante gli assiomi di Armstrong.

Def 9: Decomposizione preserva F 🟢

Sia $R$ uno schema relazionale ed $F$ un insieme di dipendenze funzionali su $R$.

Definiamo con $\rho =\{R_1,R_2,\dots ,R_k\}$ una decomposizione di $R$ (ovvero $R=R_1\cup r_2\cup \cdots \cup R_k$)

Questa decomposizione si dice che preserva R se $F\equiv {\bigcup }_{i=1}^k{\pi }_{R_i}(F)$, dove:

$$\pi R_i(F)=\{X\to Y:X\to Y\in F^{+}\wedge XY\subseteq R_i\}$$

oss: Per verificare l’equivalenza tra $F$ e $G$ , dove $G={\bigcup }_{i=1}^k{\pi }_{R_i}(F)$, ci basta verificare che $F\subseteq G^{+}$, infatti $G{\subseteq }^{+}F$ sappiamo essere vero per definizione.

Algo 2 (se $F\subseteq G^{+}$) 🟢

Questo algoritmo richiede che venga calcolato $X_G^{+}$ quindi usiamo il prossimo algoritmo per calcolarlo (Algo 3).

Algo 3 ( $X_G^{+}$) 🟢

Teorema 5 (dim algo 3) 🟢

Sia R uno schema relazionale, F un insiemi di dipendenze funzionali su R e $\rho =\{R_1,R_2,\dots ,R_k\}$ una decomposizione di R e X un sotto insieme di R.

L’algoritmo 3 calcola correttamente $X_G^{+}$, dove $G={\bigcup }_{i=1}^k\pi R_i(F)$

---

Dimostrazione

Indichiamo con $Z^{(0)}$ il valore iniziale di $Z$ (ovvero $Z^0=X$), ed in particolare con $Z^{(\text{i})}$ il valore di $Z$ dopo l’i-esima iterazione dell’assegnazione $Z=Z\cup S$.

oss: $Z^{(\text{i})}\subseteq Z^{(\text{i}+1)}$

Indichiamo con $Z^f$ il valore di $Z$ al termine dell algoritmo, proveremo che:

$$A\in Z^f\text{ se e solo se }A\in X_G^{+}$$

Parte solo se: $Z^{(f)}\subseteq X_G^{+}$

Mostreremo per induzione che su i che $Z^{(i)}\subseteq X_G^{+}$ per ogni i.

• Caso base: i = 0, abbiamo che $Z^{(0)}=X$ e $X\subseteq X^{+}$, quindi $Z^{(0)}\subseteq X_G^{+}$
• Ipotesi induttiva: $Z^{(i-1)}\subseteq X_G^{+}$

Induzione:

Per ipotesi induttiva $Z^{(\text{i}-1)}\subseteq X^{+}$

Sia A un attributo in $Z^{(\text{i})}-Z^{\text{i}-1}$ (ovvero un attributo aggiunto all’iterazione i)

Deve esistere una dipendenza un indice j tale che $A\in (Z^{(i-1)}\cap R_j{)}_F^{+}$ per questo:

• Poiché $A\in (Z^{(i-1)}\cap R_j{)}_F^{+}$ si ha che $(Z^{(i-1)}\cap R_j)\to A\in F^{+}$ (per lemma1 + Teo $F^{+}=F^A$)
• Poiché $(Z^{(i-1)}\cap R_j)\to A\in F^{+}$ e $A\in R_j$ e $Z^{(i-1)}\cap R_j\subseteq R_j$, per definizione di G si ha che $(Z^{(i-1)}\cap R_j)\to A\in G$
• Poiché per ipotesi induttiva si ha che $X\to Z^{(i-1)}\in G^{+}$, per decomposizione otteniamo $X\to (Z^{(i-1)}\cap R_j)\to A\in G^{+}$
• Quindi per transitività $X_G^{+}\subseteq G^{+}$ ovvero $A\in X_G^{+}$

Quindi $Z^{(i)}\subseteq X_G^{+}$

Def 10: Join senza perdita 🟢

Sia $R$ uno schema relazionale. Una decomposizione di $\rho$ di $R$ ha un join senza perdita se per ogni istanza legale $r$ di $R$ si ha $r={\pi }_{R_i}(r)\bowtie \cdots \bowtie {\pi }_{R_k}(r)$.

Teorema 6: Proprietà $m_{\rho }(r)$ 🟢

Sia $R$ uno schema relazionale e $\rho$ una decomposizione di $R$.

Per ogni istanza legale r di $R$, indichiamo con $m_{\rho }(r)={\pi }_{R_1}(r)\bowtie \cdots \bowtie {\pi }_{R_k}(r)$ che ha queste 3 proprietà:

1. $r\subseteq m_p(r)$, indica che il risultato del join potrebbe avere introdotto nuove tuple nelle tabella, portando a una perdita di informazioni. Il join si dice senza perdita se $r=m_{\rho }(r)$.
2. ${\pi }_{R_i}(m_{\rho }(r))={\pi }_{R_i}(r)\text{ per ogni }i$, indica che se facciamo la proiezione di qualsiasi schema $R_i$ della decomposizione sul join, otteniamo lo stesso se effettuiamo la stessa proiezione sullo istanza originale r.
3. $m_{\rho }(m_{\rho }(r))=m_{\rho }(r)$

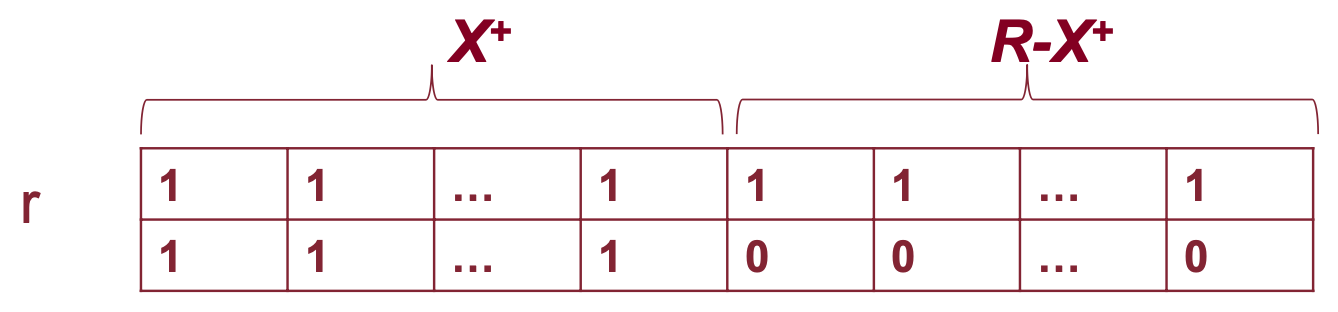
Algo 4: determina se decomposizione ha join senza perdita 🟢

• Input: Uno schema relazionale R, un insieme di Dipendenze Funzionali su R, una decomposizione $\rho =\{R_1,R_2,\dots ,R_n\}$ di R .

• Output: true se $\rho$ ha un join senza perdita.

---

L’obbiettivo è creare una tabella r e verificare che il join sia senza perdita.

Struttura dalla tabella:

• ad ogni colonna è assegnato un attributo diverso di $R$ (numero di colonne = $\mid R\mid$)
• ad ogni riga è assegnato un sotto schema diverso di $\rho$ (numero righe = $\mid \rho \mid$)

Inizializzazione dalla tabella - all’incrocio tra la riga i e la colonna j inseriamo:

• il simbolo $a_j$ se l’attributo $A_j\in R_i$
• il simbolo $b_{ij}$ altrimenti

Ora per ogni $X\to Y\in F$ se ci sono due tuple t1 e t2 in r tali che $t1[X]=t2[X]$ e $t1[Y]\ne t2[Y]$ allora per ogni $A_j$ in $Y$ (per ogni elemento della colonna Y):

• se $t_1[A_j]=a_j$ allora $t_2[A_j]:=a_j$
• altrimenti $t_1[A_j]=t_2[A_j]$

Questo ciclo si ripete fino a quando non raggiungiamo una di queste due condizioni:

1. otteniamo una riga composta da sole a ($\rho$ ha join senza perdita)
2. otteniamo un iterazione che non modifica la tabella ($\rho$ non ha un join senza perdita)

---

Versione Prof.

Teorema 7: Dimostrazione Tabella 🟢

Sia R uno schema di relazione, F un insieme di dipendenze funzionali su R e $\rho =\{R_1,R_2,\dots ,R_k\}$ una decomposizione di R.

L’Algoritmo 4 determina correttamente se $\rho$ ha un join senza perdita.

---

Occorre dimostrare che:

$$\begin{array}{rl}\rho \text{ ha un jo}& \text{in senza perdita}\\ & ⟺\\ \text{quando l’algoritmo termina}& \text{ la tabella r ha una tupla con tutte ’a’}\end{array}$$

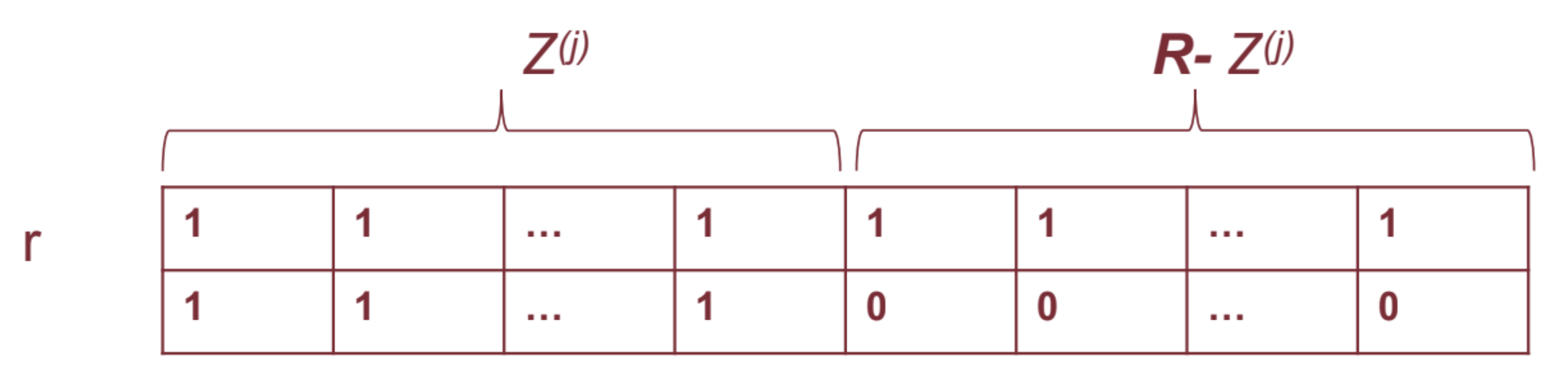
oss: La tabella r può essere interpretata come un’istanza legale di R, in quanto l’algoritmo termina quando non ci sono più violazioni delle dipendenze in F. Infatti basta sostituire ai simboli 'a' e 'b' valori presi dai domini dei corrispondenti attributi in modo tale che ad uno stesso simbolo venga sostituito lo stesso valore.

Dimostrazione parte solo se ovvero:

$$\rho \text{ ha un join senza perdita}⟹\text{ la tabella r ha una tupla con tutte ’a’}$$

Supponiamo per assurdo che $\rho$ abbia un join senza perdita e che quando l’algoritmo termina la tabella r non abbia una tupla con tutte a.

Poiché nessun simbolo a che compare nella tabella costruita inizialmente viene mai modificato dall’algoritmo, abbiamo che:

• Per ogni i ($i=0,\dots ,1$) ${\pi }_{R_i}(r)$ contiene una tupla con tutte a
• Pertanto $m_{\rho }(r)$ contiene una tupla con tutte a e, quindi, $m_{\rho }(r)\ne r$ (contraddizione).

Def 11: Copertura minimale 🟢

Sia F un insieme di dipendenze funzionali, una copertura minimale di F è un insieme G di dipendenze funzionali equivalente ad F tale che:

1. Ogni dipendenza in G ha la parte destra singleton
2. Per nessuna dipendenza $X\to A\in G$ esiste un $X^{\prime }\subseteq X$ tale che $G\equiv G-\{X\to A\}\cup \{X^{\prime }\to A\}$
3. Per nessuna dipendenza $X\to A\in G$ deve accadere $G\equiv G-\{X\to A\}$.

Ovvero:

• (1) Si capisce daii

• (2) Gli attributi a sinistra non devono essere ridondanti, ovvero non devono esistere dipendenze funzionali in G tali che se sostituiamo il determinante con un suo sotto insieme, otteniaamo chr G rimane equivalente a prima.

• (3) Le dipendenze funzionali non devono essere ridondanti, ovvero non deve esistere una dipendenza in G che se rimossa, otteniamo che G rimane equivalente a prima.

oss: La copertura non è unica, ovvero per una data F possono esiste più comperture minimali

Algo 5 (calcolo di $\rho$) 🟢

Algoritmo che calcola in tempo polinomiale una decomposizione $\rho$.

Input:

• uno schema relazionale R
• un insieme di dipendenze funzionali F su R (che è anche una copertura minimale)

Output: una decomposizione $\rho$ di R che:

• preserva F
• ogni schema di relazione in $\rho$ è in 3NF

oss:R può avere anche più di una decomposizione valida, dato che possono esistere diverse coperture minimali G su R.

Teorema 8 🟢

Sia R uno schema di relazione ed F un insieme di dipendenze funzionali su R, che è una copertura minimale.

L’algoritmo 5 permette di calcolare in tempo polinomiale una decomposizione $\rho$ di R tale che:

• ogni schema di relazione in $\rho$ è in 3NF
• $\rho$ preserva F.

---

Dimostrazione: $\rho$ preserva $F$

• F è la copertura minimale presa in input dall’algoritmo
• Sia G l’insieme delle dip. funzionali preservate dal $\rho$, appena calcolato dal algoritmo, ovvero $G={\bigcup }_{i=1}^n{\pi }_{R_i}(F)$

L’obbiettivo è dimostrare che $F\equiv G$, ovvero che $F\subseteq G^{+}$ e $G\subseteq F^{+}$.

$\text{ Dim. }F\subseteq G^{+}$ - Per ogni dipendenza funzionale $X\to A\in F$ l’algoritmo crea un sottoschema $XA\in \rho$ e si ha che $X\to A\in G$, di conseguenza otteniamo che $F\subseteq G⟹F\subseteq G^{+}$.

$\text{ Dim. }G\subseteq F^{+}$ - L’inclusione $G\subseteq F^{+}$ è banalmente verificata in quanto, per definizione, $G\subseteq F+$

Quindi $F\equiv G$

---

Dimostrazione: ogni schema di relazione in $\rho$ è in 3NF

Ci sono tre modi in cui un sotto schema può essere inserito in $\rho$:

Metodo 1: se $S\in \rho$ allora ogni attributo di $S$ non partecipa ad una dipendenza funzionale in F, quindi $S$ è chiave su S, quindi banalmente è in 3NF.

Metodo 2:

Metodo 3:

Se $XA\in \rho$ allora:

• $X\to A\in F$, ma dato che $F$ è una copertura minimale allora non esiste $X^{\prime }\to A\in F$ tale che $X^{\prime }\subseteq X$
• quindi $X$ è chiave in $XA$ e $X\to A\in F$ non falsifica la 3NF di $XA\in \rho$, dato che X è superchiave.

Se esiste $Y\to B\in F^{+}$ tale che $YB\subseteq XA$, allora neanche questa falsificherebbe la 3NF di $XA\in \rho$, dato che:

• se $B=A$ allora, poiché $F$ è una copertura minimale, $Y=X$ e quindi Y è superchiave.
• se $B\ne A$ allora $B\in X$ e quindi B è primo.

Definizione 12 🟢

Uno schema è in forma normale Boyce-Codd se per ogni dipendenza funzionale $X\to A\in F^{+}$ tale che $A\notin X$ si ha che $X$ è una superchiave.

Se uno schema è in Boyce Codd allora è anche in 3NF ma non è vero il contrario.

Non esiste sempre una decomposizione che:

• Tutti schemi in Boyce Codd
• preserva F
• Join senza perdita

Invece esiste sempre:

• Tutti schemi in Boyce Codd
• Join Senza perdita. Ed esiste anche un algoritmo che genera tale decomposizione.