Connettivi logici

---

Indice

Le proposizioni semplici sono composte per mezzo dei connettivi logici:

1. Congiunzione
2. Disgiunzione
3. Negazione
4. Implicazione
5. Doppia Implicazione
6. Joint denial (NOR)
7. Alternative denial (NAND)

Altro:

• Tavole di verità
• Precedenze
• Interdipendenze dei connettivi

---

Congiunzione

• Scritture: ∧, et, AND, e
• Significato: a ∧ b è vera se lo è sia a che b;

---

Disgiunzione

• Scritture: ∨, vel, OR, o
• Significato: a ∨ b è vera quando lo è almeno uno fra a e b;

---

Negazione

• Scritture: ¬, ∼, non, NOT
• Significato: ¬a è vera quando a è falsa;

---

Implicazione

• Scritture: ⇒, se … allora
• Significato: a → b ≡ ¬a ∨ b
• a viene detta premessa e b conseguenza;

---

Doppia Implicazione o Equivalenza

• Scritture: ↔, ≡,se e solo se, equivalente
• Significato: a ↔ b ≡ (a → b) ∧ (b → a) ≡ (a ∧ b) ∨ (¬a ∧ ¬b).

---

Joint denial (NOR)

• Scritture: ↓, NOR
• Significato: a ↓ b è vera se a e b sono entrambe false

---

Alternative denial (NAND)

• Scritture: | , NAND
• Significato: a | b è vera in tutti i casi tranne quando a e b sono entrambe false

---

Tavole di verità

---

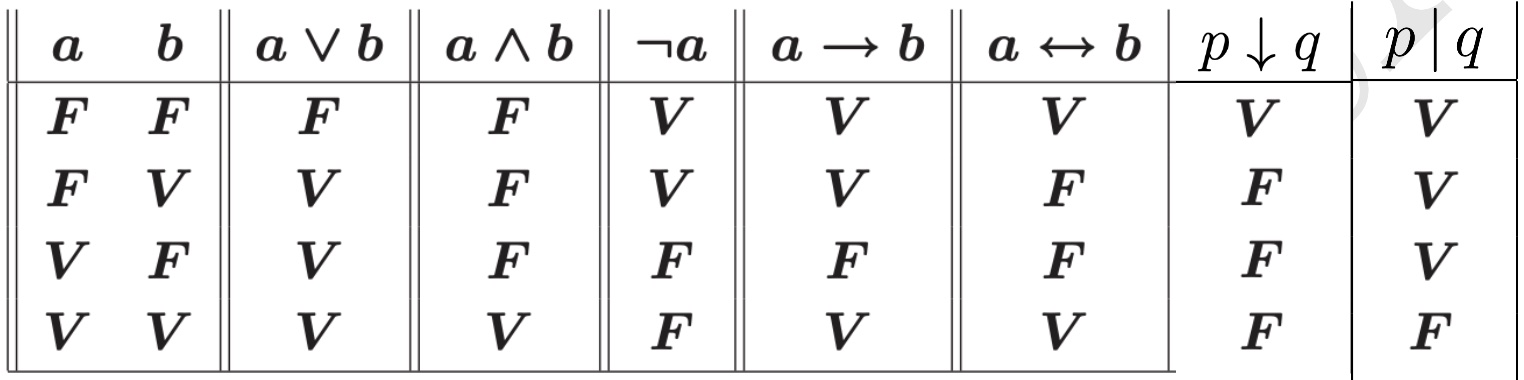
Precedenze

Le precedenze permettono di ridurre il numero di parentesi necessarie per interpretare correttamente una proposizione.

¬ precede ∧ precede ∨ precede → precede ↔

Esempi:

• ((¬a) ∨ a) si può scrivere ¬a ∨ a
• (a ∨ (b ∧ c)) si può scrivere a ∨ b ∧ c
• (a ∧ (b ∨ c)) si può scrivere a ∧ (b ∨ c)

---

Interdipendenze dei connettivi

• p → q ≡ ¬p ∨ q
• p ∧ q ≡ ¬( ¬p ∨ ¬q)
• p ←> q ≡ ( p → q ) ∧ ( q → p) o anche ( p ∧ q ) ∨ ( ¬ p∧ ¬ q)
• p ↓ p ≡ ¬( p ∨ q )

---