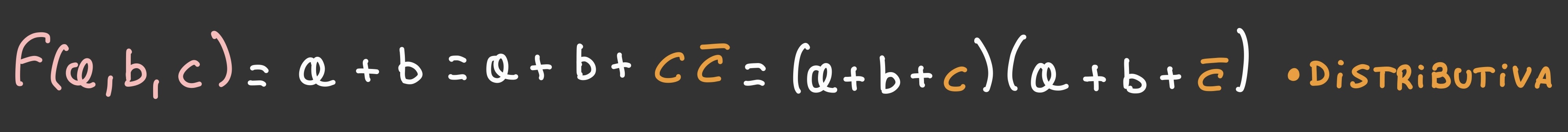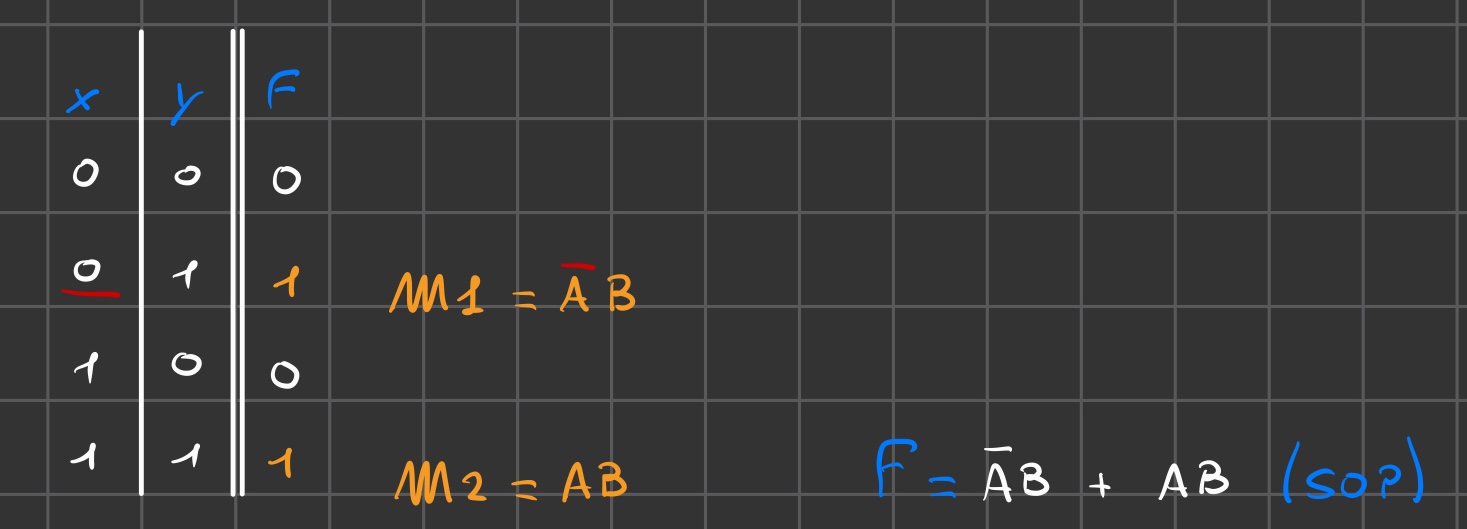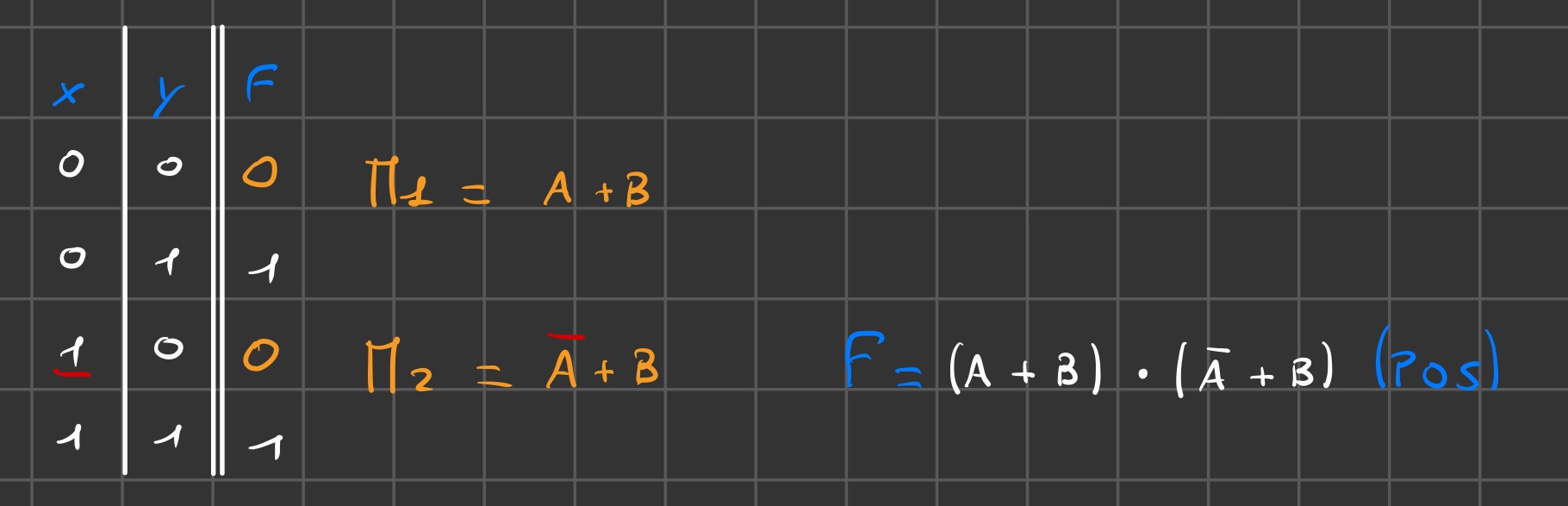Index
Related
Forma normale
Sop (forma normale disgiuntiva)
- rete: and-to-or
Pos (forma normale congiuntiva)
- rete: or-to-and
OSS: forma normale != forma minimale
Come ottenere forma normale
Metodo
- Applicare leggi di demorgan (fino ad ottenere la complementazione sulle singole variabili)
- Proprietà distributiva
- Eliminare termini ripetuti (usare idempotenza)
Forma canonica
Sop (forma canonica disgiuntiva)
- Tutti i termini prodotto sono min-termini
Pos (forma canonica congiuntiva)
- tutti i termini somma sono max-termini
Come ottenere forma canonica
Forma normale ⇒ Forma canonica
Forma canonica SOP:
- Moltiplicare il termine prodotto in cui manca x per (x+!x)
Forma canonica POS:
- sommare al termine somma in cui manca x il prodotto x!x
Tabella di verità ⇒ Forma canonica
Forma canonica SOP
- Calcolare la funzione trovando i mintermini:
Min-termine (1)
Definizione
Un termine prodotto in cui compaiono letterali corrispondenti a tutte le variabili della funzione e tale per cui la configurazione di valori delle variabili definite dai letterali genera un valore 1 della funzione stessa nella tabella delle verità, costituisce un mintermine della funzione
OSS: se valore variabile = 0 allora nel mintermine la variabile è negata
Calcolo funzione
Unire mintermini con somme logiche (forma sop)
Link to originalForma canonica POS
- Calcolare la funzione trovando i max-termini:
Max-termine (0)
Definizione
Un termine somma in cui compaiono letterali corrispondenti a tutte le variabili della funzione e tale per cui la configurazione di valori delle variabili definite dai letterali genera un valore 1 della funzione stessa nella tabella delle verità, costituisce un mintermine della funzione
OSS: se valore variabile = 1 allora nel mintermine la variabile è negata
Calcolo funzione
Unire mintermini con somme logiche (forma sop)
Link to original
Consigli