Metodo dei Tableaux nella logica proposizionale

---

Indice:

1. Obbiettivo
2. Metodo
3. Sviluppare una formula
4. α o β
5. Chiudere una ramo
6. Consigli

---

Obbiettivo

Il metodo dei tableaux è un metodo dimostrativo utilizzato per verificare se una determinata formula è una tautologia.

---

Metodo

Per dimostrare che una determinata formula (F) è una tautologia dobbiamo vedere se non esiste alcuna interpretazione che rendere vera la negazione della formula (¬F)

1. Negare F
2. Sviluppare ¬F
3. Continuare a sviluppare le semplificazioni (sotto formule) di ¬F …
4. Fermarsi quando si è raggiunta la semplificazione massima ho si è riuscito a chiudere tutti i rami

Fine:

• Se non è stato possibile chiudere tutti i rami significa che esiste una o più interpretazioni di ¬F vere quindi F non è una tautologia
• Se è stato possibile chiudere tutti i rami allora ¬F è una contraddizione e F è una tautologia

---

Sviluppare una formula

• Sviluppare una formula significa scomporla nelle sotto formule che la compongono

  • es: x ∨ y è composta da x e y

• Lo sviluppo di una formula o sotto formula può dare due risultati:

1. Uno “stack” , generato da una formula α (alpha) composta da α1 e α2 (sotto-formule) posizionate una sopra all’altra
   • oss: una formula α si può anche chiamare “formula di tipo AND”
2. Un “Ramo”, generato da una formula β (beta) composta da β1 e β2 (sotto-formule) che si dividono in due rami
   • oss: una formula β si può anche chiamare “formula di tipo OR”

---

α o β

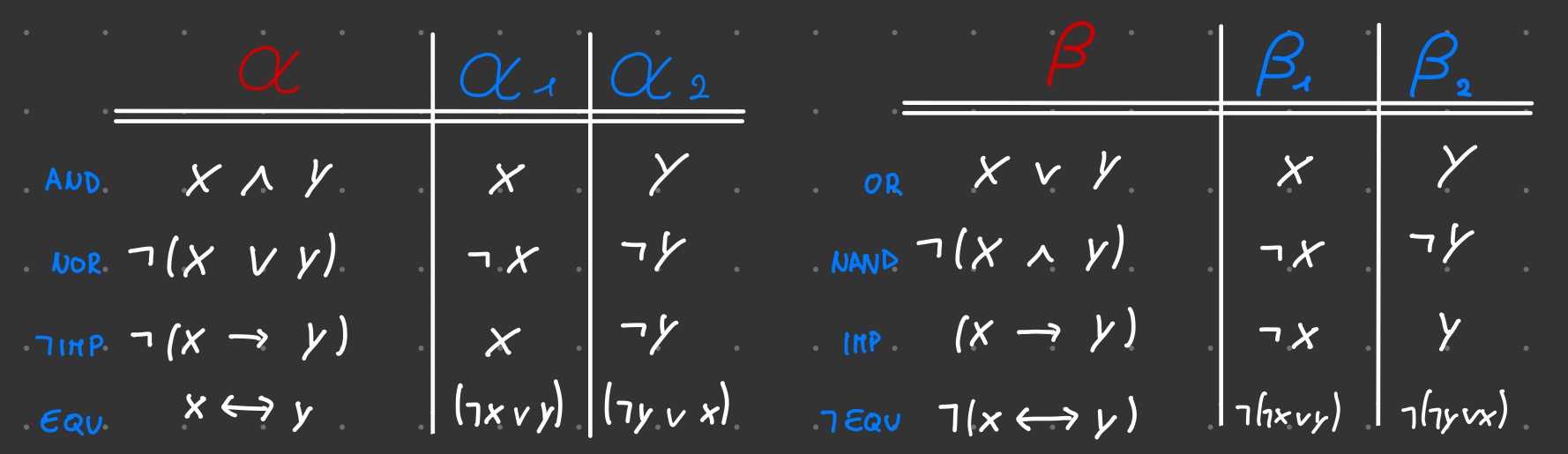
Nota

$\begin{array}{lcl}\neg (A\wedge B)& =& \neg A\vee \neg B\\ \neg (A\vee B)& =& \neg A\wedge \neg B\\ \neg (\neg A)& =& A\\ \neg (A\Rightarrow B)& =& A\wedge \neg B\\ A\Rightarrow B& =& \neg A\vee B\\ A\iff B& =& (A\wedge B)\vee (\neg A\wedge \neg B)\\ \neg (A\iff B)& =& (A\wedge \neg B)\vee (\neg A\wedge B)\end{array}$

oss:

& 1)\ \ \ x \implies y \equiv \neg x \lor y\\ \\ & 2)\ \ \ x \iff y\equiv (x \implies y) \land (y \implies x)\\ \\ & 3)\ \ \ x \iff y\equiv (\neg x \lor y) \land (\neg y \lor x)\\ \end{align}$$ --- ## Chiudere una ramo - chiudere un ramo significa non continuare a semplificare (scomporre) un ramo del tableaux perché si è incontrata una contraddizione ***Esempio:*** ![[Screenshot 2023-11-21 at 15.23.42.png|700]] Se si riesce a chiudere tutti i rami allora abbiamo dimostrato che la formula originale è una tautologia --- ## Consigli 1. Nello svolgimento di un tableaux si ha libertà su quale parte dello stack o quale ramo svolgere prima. - Solitamente è più veloce risolvere le formule *α* (AND) rispetto alle formule *β* (OR), infatti ogni volta che risolviamo una formula *β* (OR) creiamo 2 rami raddoppiando il numero di operazioni necessarie ---