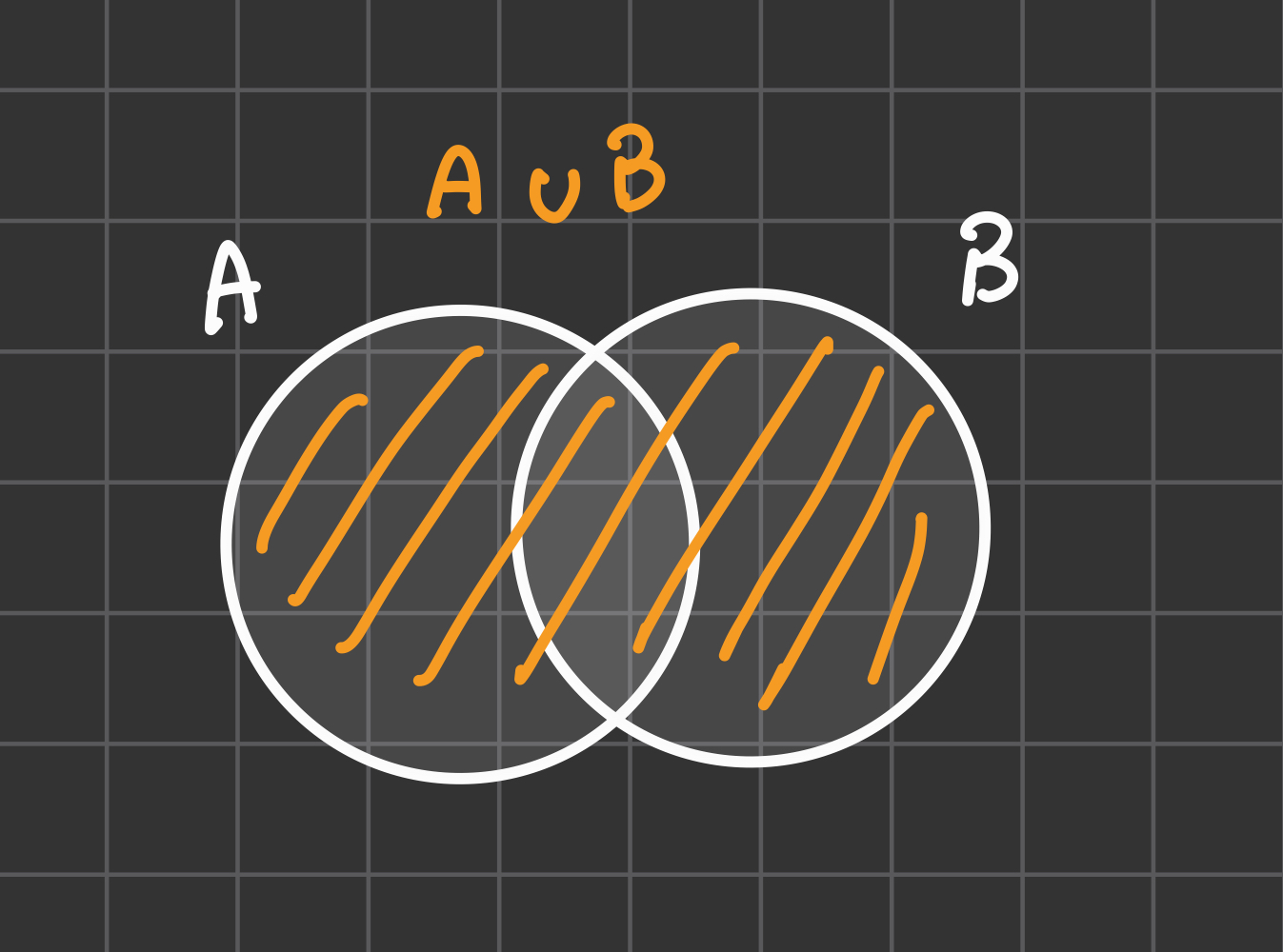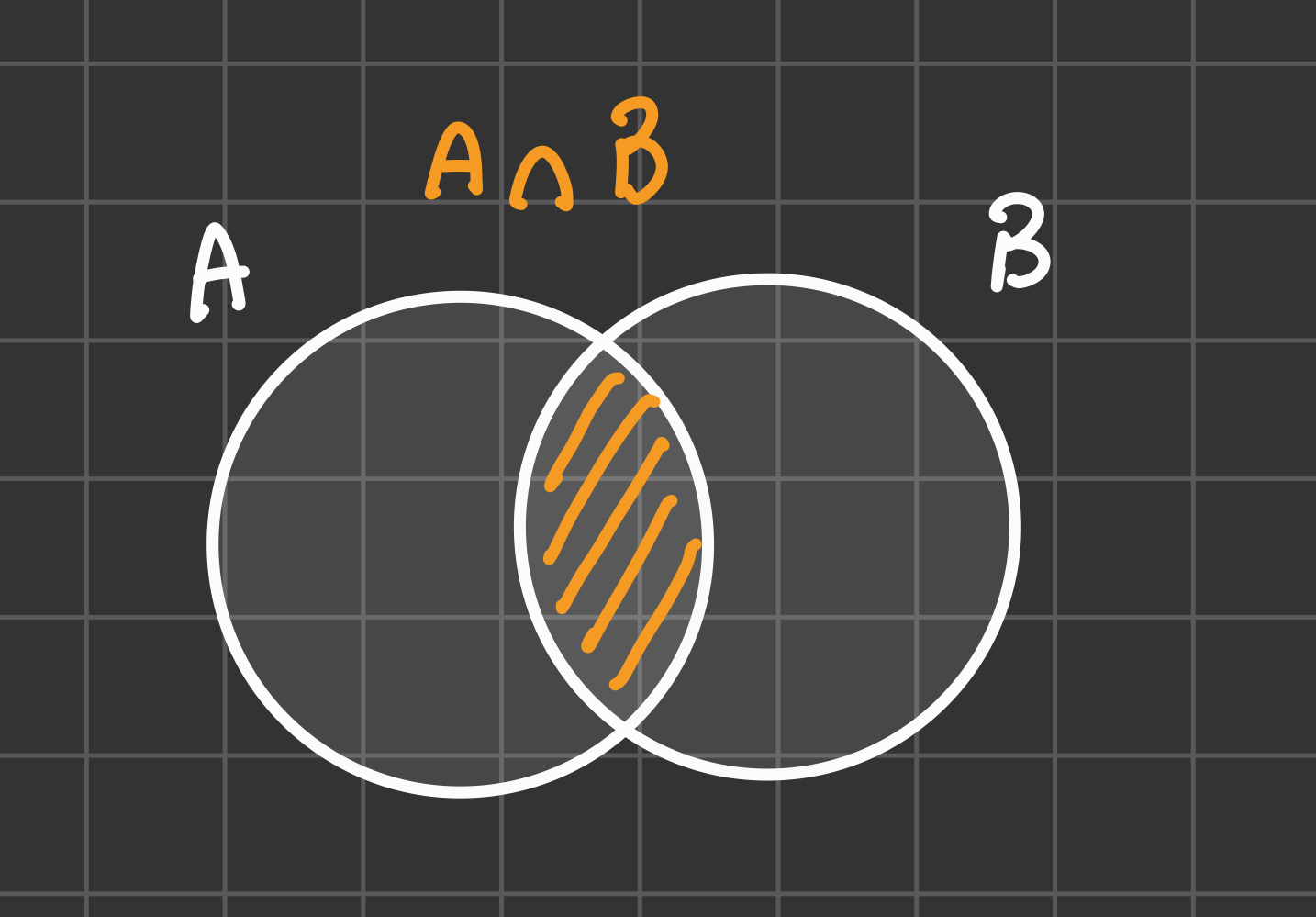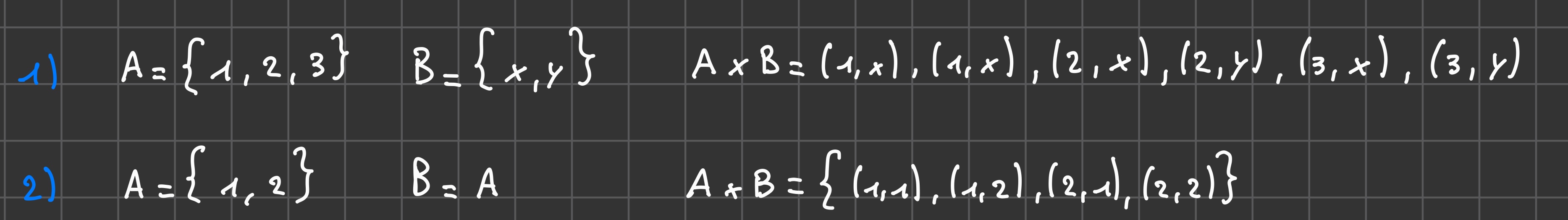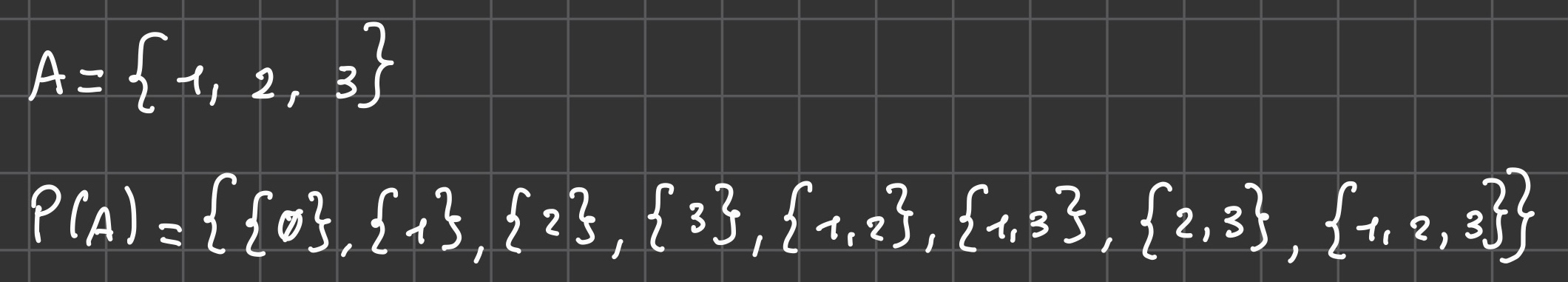Operazioni sugli insiemi

Index

1. Appartenenza
2. Inclusione
3. Unione
4. Intersezione
5. Differenza
6. Complemento
7. Prodotto cartesiano
8. Insiemi delle parti

Related

• Teoria degli insiemi

---

Appartenenza

Definizione

$$x\in A$$

Significato: x è elemento che appartiene ad A.

---

Inclusione

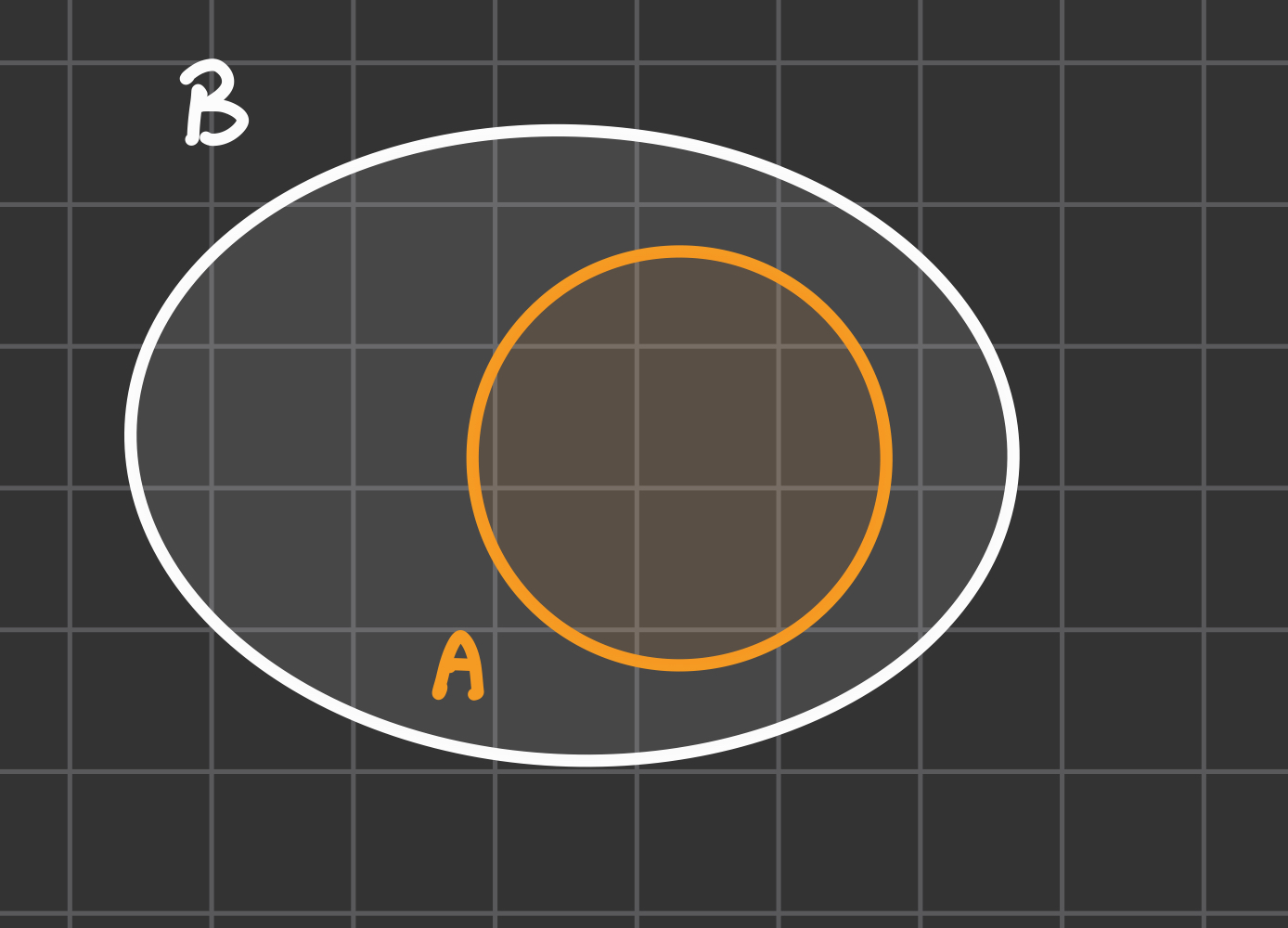
Sottoinsieme proprio o inclusione stretta

$$A\subset B$$

Significato: Sottoinsieme A è contenuto nell’insieme B, ma esiste almeno un elemento di B che non è contenuto in A.

Sottoinsieme improprio

$$A\subseteq B$$

Significato: Nell’inclusione normale (A⊆B) invece i due insiemi possono anche essere uguali (A=B).

oss: $A=B⟺(A\subseteq B)\wedge (B\subseteq A))$

---

Unione

Definizione

$$A\cup B=\{x:x\in A\text{ oppure }x\in B\}$$

Significato: Un elemento o appartiene ad A o appartiene a B.

Proprietà

$$\begin{array}{rl}& 1.A\cup \varnothing =A\\ & 2.A\cup B=B\cup A\text{ (Commutativa)}\\ & 3.(A\cup B)\cup C=A\cup (B\cup C)\text{ (Associativa)}\\ & 4.A\cup A=A\\ & 5.B\subseteq A⟹A\cup B=A\end{array}$$

---

Intersezione

Definizione

$$A\cap B=\{x:x\in A\text{ e }x\in B\}$$

Significato: Un elemento appartiene sia ad A che a B.

Vedi: Principio di Inclusione ed Esclusione

Proprietà

$$\begin{array}{rl}& 1.A\cap \varnothing =\varnothing \\ & 2.A\cap B=B\cap A\text{ (Commutativa)}\\ & 3.(A\cap B)\cap C=A\cap (B\cap C)\text{ (Associativa)}\\ & 4.A\cap A=A\\ & 5.B\subseteq A⟹A\cap B=B\end{array}$$

---

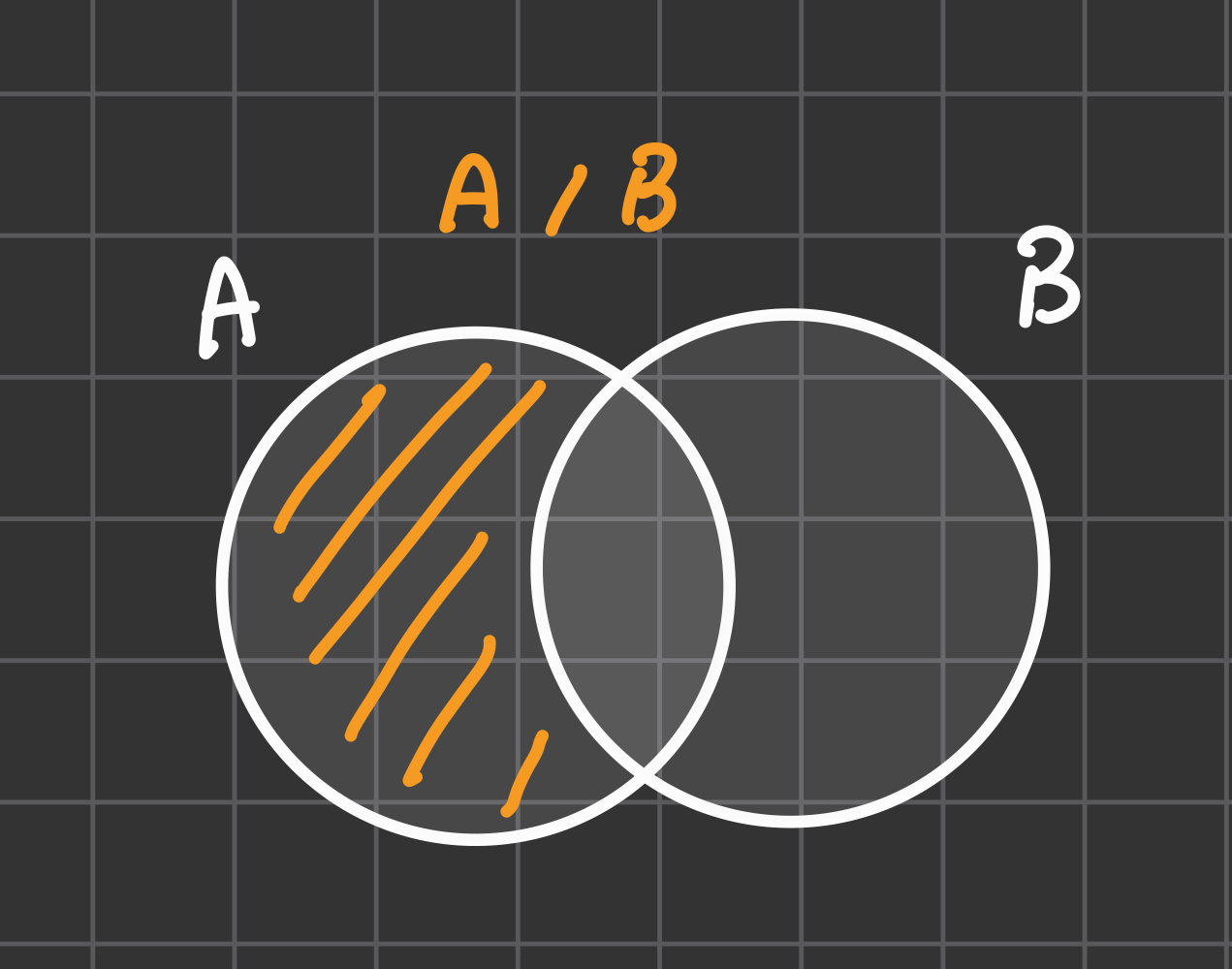
Differenza

Definizione

$$A\setminus B==\{x:x\in A\text{ e }x\notin B\}$$

Significato: Un elemento appartiene ad A ma non a B.

Osservazione

$$A-B\ne B-A$$ $$seA=B⟹A-B=\{\varnothing \}$$

---

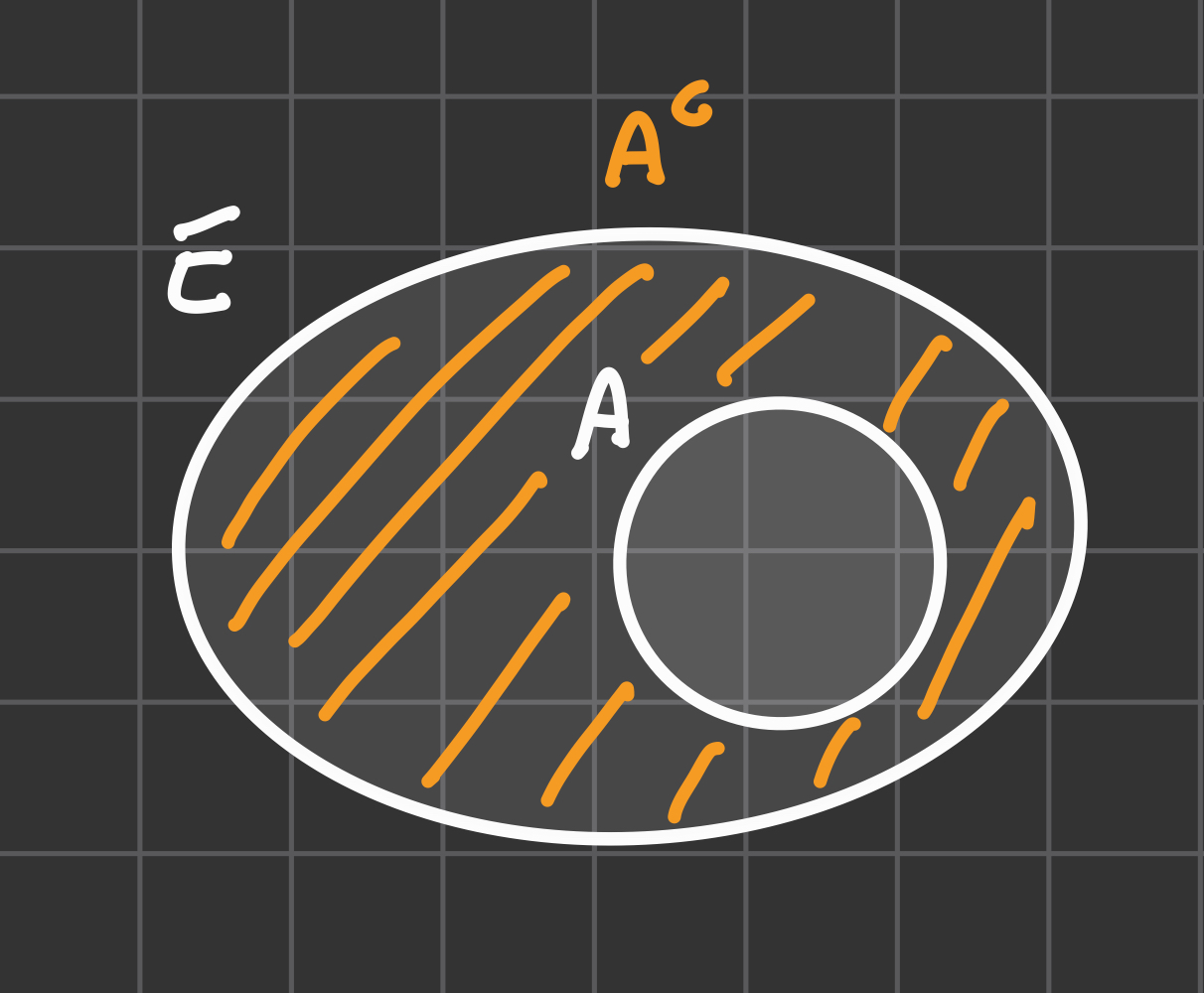
Complemento

Definizione

$$A^C:=\{x\in E:x\notin A\}$$

Significato: Dato un insieme A sotto insieme di E (insieme universo E), si definisce insieme complementare di A, l’insieme degli elementi che non appartengono ad A ma che sono contenuti in E.

Osservazione

$$\begin{array}{rl}& \\ & \text{se }A\subseteq E⟹A^C=E/A\end{array}$$

---

Prodotto cartesiano

Definizione

$$A\times B=\{(a,b)|a\in A,b\in B\}$$

Significato: Prodotto cartesiano tra gli insiemi A e B è l’insieme che ha per elementi tutte le possibili coppie ordinate (a, b).

Dove:

• a sono tutti gli elementi dell’insieme A
• b sono tutti gli elementi dell’insieme B

Esempio

---

Insiemi delle parti

Definizione

$P_A=\{B|B\subset A\}$

Significato: L’insieme delle parti di A è l’insieme che ha come elementi tutti i possibili sottoinsiemi dell’insieme A.

Osservazione

$$\begin{array}{rl}& A\in P(A)\\ & \varnothing \in P(A)\end{array}$$ $$\begin{array}{rl}& -\text{Cardinalitaˋ P(A)}=2^n\\ & -\text{Dove n eˋ la cardinalitaˋ di A}\end{array}$$

Esempio