Ricerca Ponti - Grafi

Introduzione

Definizione Ponte

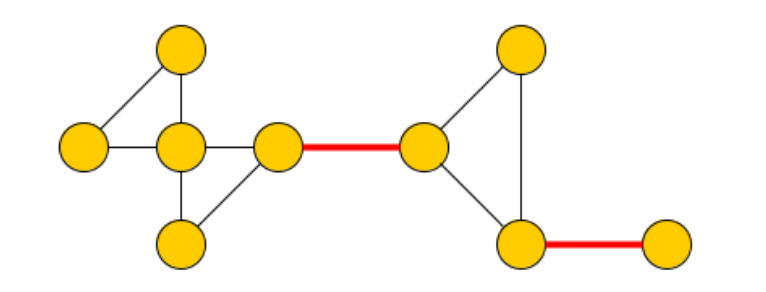
Un arco la cui eliminazione disconnette il grafo è detto ponte.

I ponti rappresentano criticità del grafo ed è quindi utile identificarli.

Numero di Ponti

In un grafo possiamo avere da 0 ad m ponti, dove:

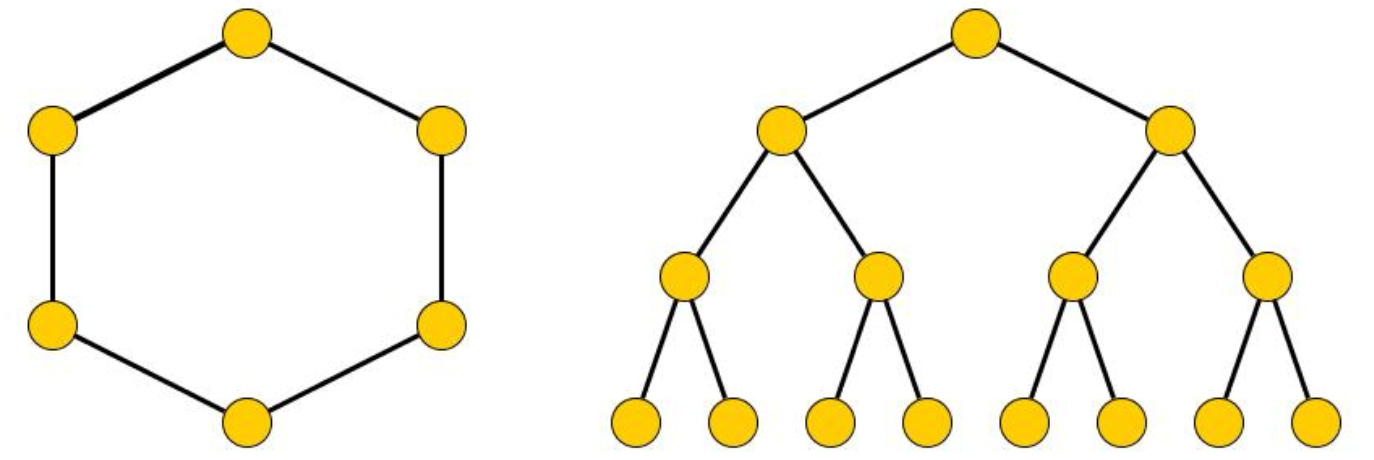
• un ciclo a 0 ponti
• un albero ha m ponti

Ricerca dei Ponti

Problema: dato un grafo connesso G determinare l’insieme di ponti del grafo.

Soluzione Esaustiva

Una soluzione potrebbe essere effettuare una ricerca esaustiva, quindi per effettuiamo una prova per verificare se è un arco o meno. Questo prova consiste nell’eliminare l’arco e verificare se il grafo ottenuto è connesso o meno.

Questa soluzione però richiede $m\cdot O(m)=O(m^2)=O(n^4)$, dove:

• m numero di volte che dobbiamo effettuare la prova (per ogni arco)
• O(m) costo della prova (controllo se grafo è conesso)

È possibile risolvere questo problema in tempo lineare ma richiede un osservazione:

Osservazione

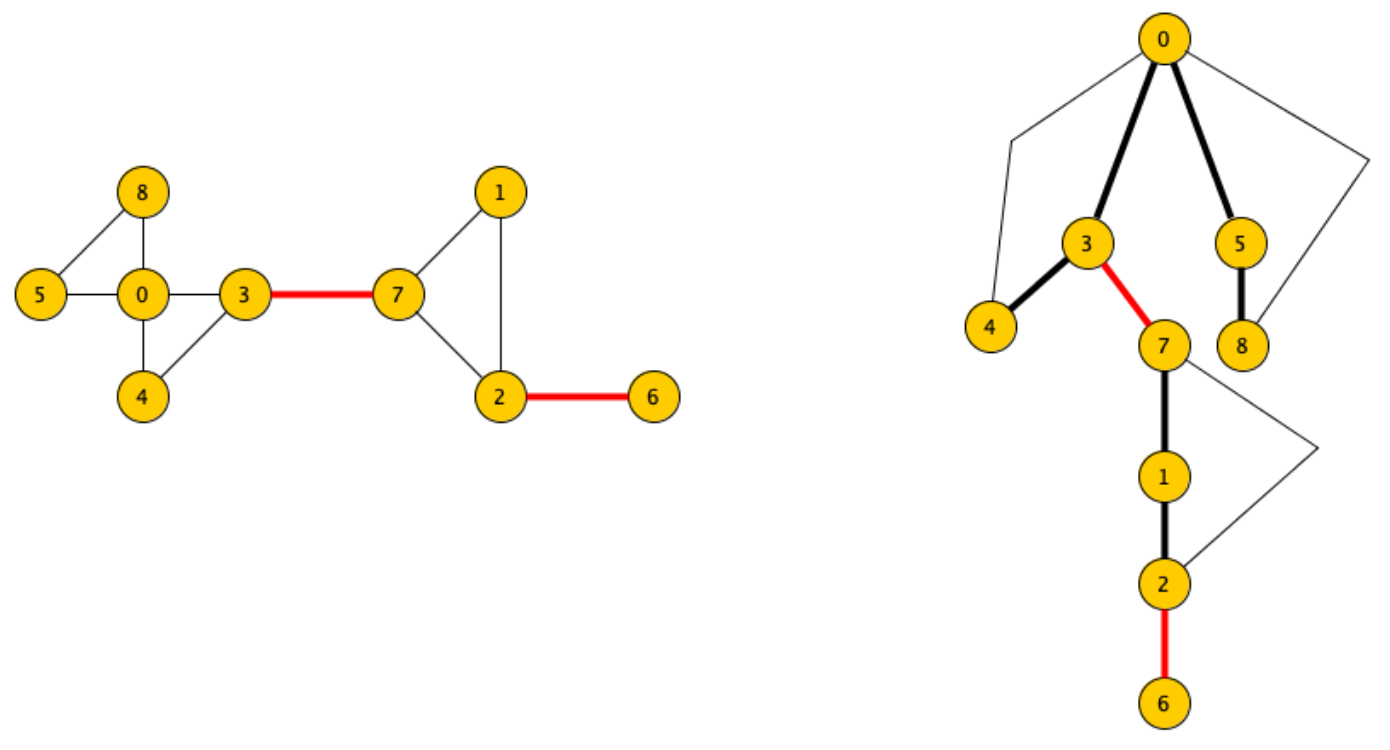
I ponti del grafo possono essere ricercati unicamente tra gli n − 1 archi dell’albero DFS.

Infatti un arco non presente nel albero DFS non può essere ponte, questo perché se eliminato gli altri archi dell’albero DFS continuano a garantire la connessione del grafo.

Come si può osservare gli archi dell’albero che non sono ponti risultano coperti dagli archi che non sono stati attraversati.

Soluzione Lineare

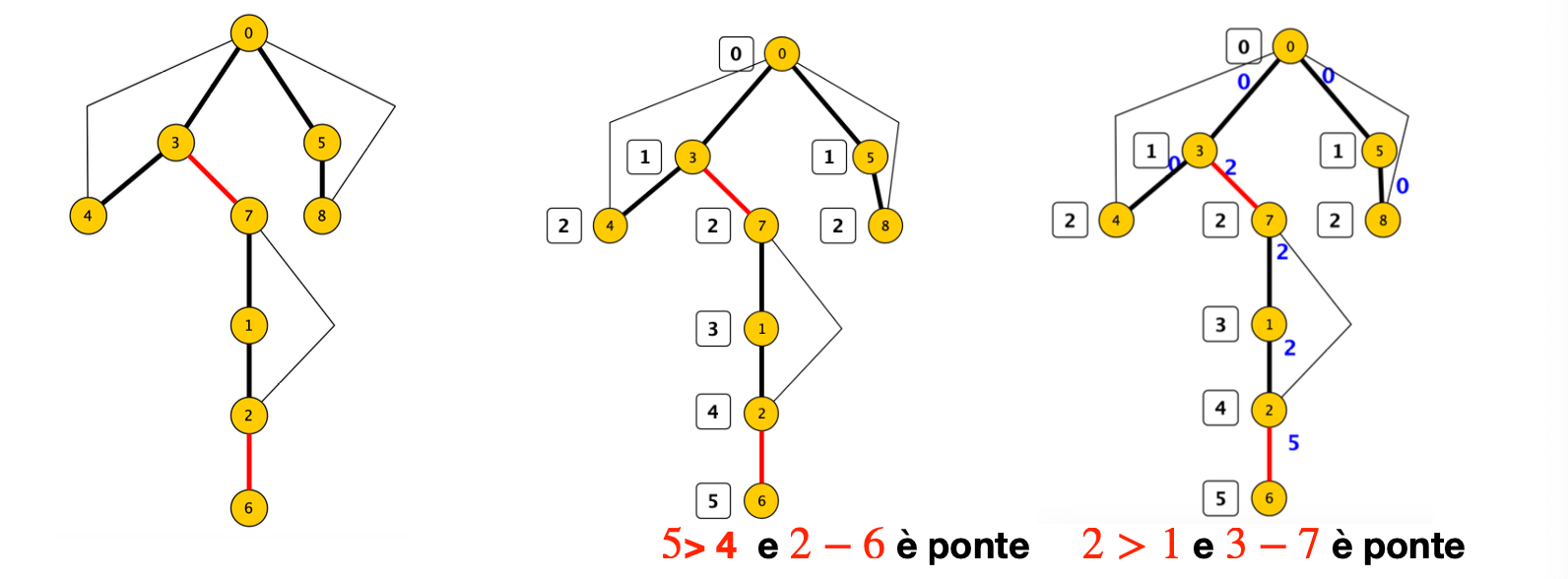
Se prendiamo (u,v) un arco dell’albero DFS con u padre e v figlio, l’arco è un ponte se e solo se non ci sono altri archi tra i nodi del sottoalbero radicato in v e il nodo u o antenati di u.

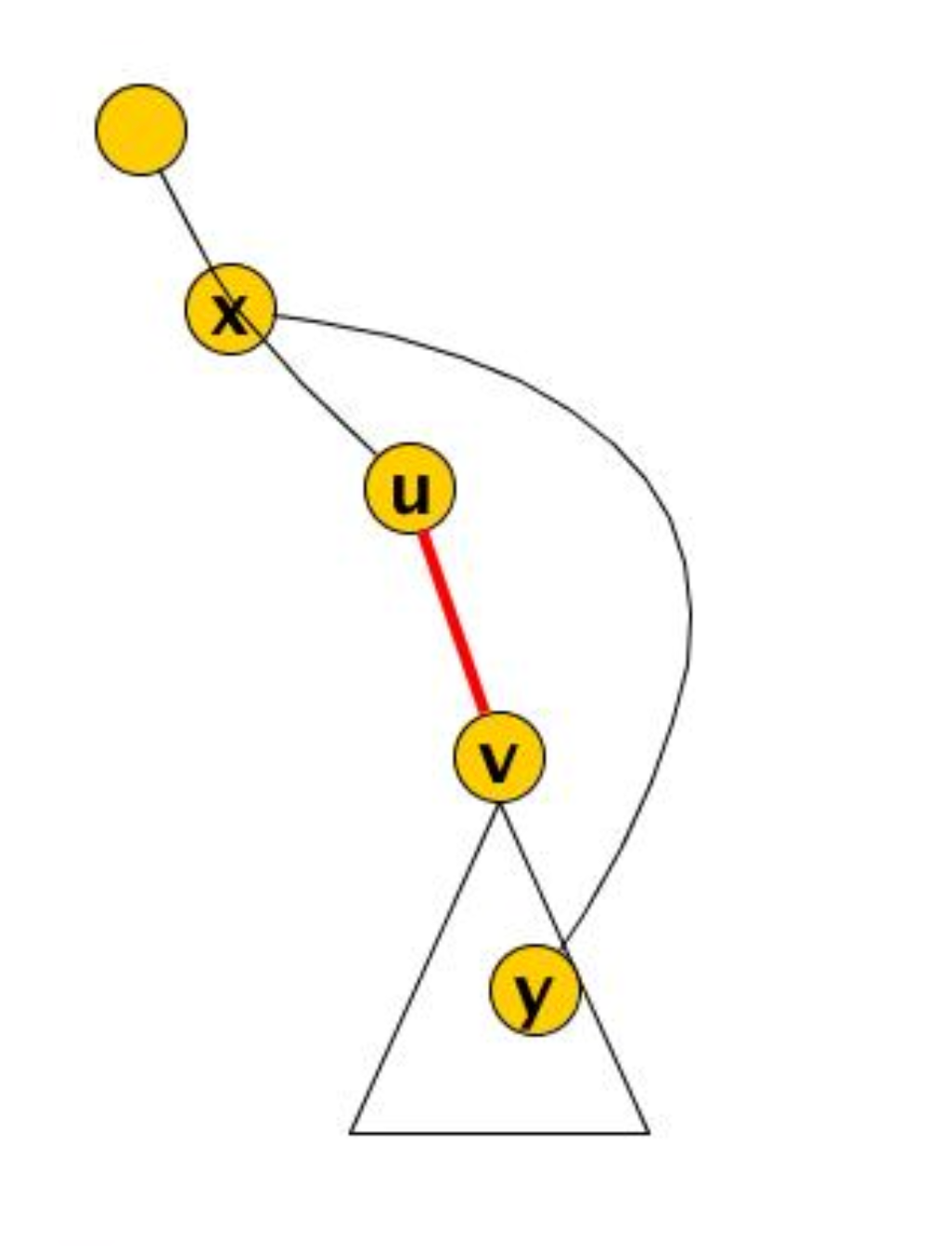
Possiamo notare che quando attraversiamo l’arco (u,v) per raggiungere v, il nodo u non può sapere se ci saranno archi che portano a suoi antenati ma può scoprirlo successivamente se v una volta terminata la sua ricerca gli restituisce le giuste informazioni.

Quindi, per ogni arco padre figlio (u,v) presente nell’albero DFS il nodo u è in grado di scoprire se l’arco (u,v) è ponte o meno usando questa strategia:

Ogni nodo v:

• Calcola la sua altezza nell’albero
• Calcola e restituisce al padre l’altezza minima che si può raggiungere con archi che partono dai nodi del suo sottoalbero diversi dall’arco (u,v).

def trova_ponti(G):
	'''
	Trova tutti i ponti in un grafo connesso non orientato G.
	G è rappresentato come una lista di adiacenza.
	Restituisce una lista di coppie (u, v) che sono ponti.
	'''
	
	altezza = [-1] * len(G) # Array memorizza altezza nodi nella DFS
	ponti = []
	dfs(0, -1, altezza, ponti)
	return ponti

def dfs(x, padre, altezza, ponti)
	'''
	Algoritmo che calcola:
		- l'altezza di ogni nodo
		- i ponti del grafo
	
	Ritorna l'altezza minima raggiungibile da x 
	ottenuta non passando per il padre
	'''
 
	# Calcolo altezza nodo corrente (x)
	if padre == -1: 
		altezza[x] = 0
	else:
		altezza[x] = altezza[padre]	+ 1
 
	# altezza minima raggiungibile dal nodo x escludendo il padre
	min_ragiungibile = altezza[x] 
	
	for y in G[x]:                        # y sono i figli di x
		if altezza[y] == -1:              # se y ancora non visitato
			b = dfs(y, x, altezza, ponti) # b = min_altezza raggiungibile da y
			if b > altezza[x]:            # altezza x minore altezza y
				ponti.append((x,y))       # quindi arco (x,y) è un ponte
			
			min_ragiungibile = min(min_ragiungibile, b)
	
		elif y != padre:
			# y già visitato, quindi (x,y) è un arco all'indietro
			min_raggiungibile = min(min_ragiungibile, altezza[y])
	
	return min_ragiungibile

Complessità

La complessità temporale della procedura è $O(n+m)$, questo perché si basa sul funzionamento della DFS.