Ripasso Iniziale di Algo 1

Efficenza di un Algoritmo

Un algoritmo si dice efficiente se la sua complessità è di ordine polinomiale nella dimensione $n$ dell’input, ovvero di complessità $O(n^c)$ dove $c$ è una costante.

Un algoritmo si dice inefficiente se la sua complessità è di ordine super-polinomiale:

• esponenziale - funzione di ordine $\Theta (c^n)=2^{\Theta (n)}$
• super-esponenziale - cresce più velocemente di un esponenziale, ad esempio $2^{\Theta (n^2)}$ o $2^{\Theta (n\log n)}$.
• sub-esponenziale - cresce più lentamente di un esponenziale, ovvero $2^{O(n)}$ ad esempio $2^{\Theta (\log n)}$ oppure $2^{\Theta (n^c)}$

Nel mondo reale sono molto pochi gli algoritmi sub-esponenziali e per questo sono molto studiati, infatti solitamente o un algoritmo è polinomiale o è esponenziale/super-esponenziale.

Caso studio Test Primalità

Una caso studio è il problema del test di primalità (determinare se un numero è primo o meno).

Un algoritmo banale, per la risoluzione di questo problema, che apparentemente potrebbe richiedere $O(n)$ consiste nel testare tutti i numeri più piccoli e vedere se ne esiste uno (diverso da 1) che lo dividere.

In realtà quest’approccio ha un costo esponenziale, perché è vero che richiede $O(n)$ operazioni ma la dimensione in input è $\log n$, poiché il numero n può essere rappresentato in binario con $\log n$ bit. Un algoritmo efficiente per risolvere questo problema dovrebbe avere complessità $O({\log }^{c}n)$.

Fin dagli anni 70 erano noti per questo problema algoritmi sub-esponenziali ad esempio di complessità $(\log n{)}^{\Theta (\log \log n)}$. Ed erano noti algoritmi probabilistici (con una piccolissima percentuale di errore) di complessità polinomiale $O({\log }^{3}n)$

Nel 2004 è stato trovato un algoritmo deterministico (senza errore) con con complessità polinomiale $O({\log }^{3}n)$.

Nel mondo reale si continuano ad utilizzare gli algoritmi probabilistici, per risolvere questo problema (nonostante il marginel’errore), perché anche se asintoticamente uguali quello probabilistico è più veloce per valori che si utilizzano nel mondo reale.

Asintoticamente più veloce != realmente più veloce

Sì, è vero. A volte, algoritmi con una complessità asintotica più bassa possono essere più lenti nella pratica rispetto ad algoritmi con una complessità asintotica più alta, a causa delle costanti nascoste nella notazione Big O.

La complessità asintotica e la velocità effettiva di un algoritmo è valida solo per valori di n sufficientemente grandi.

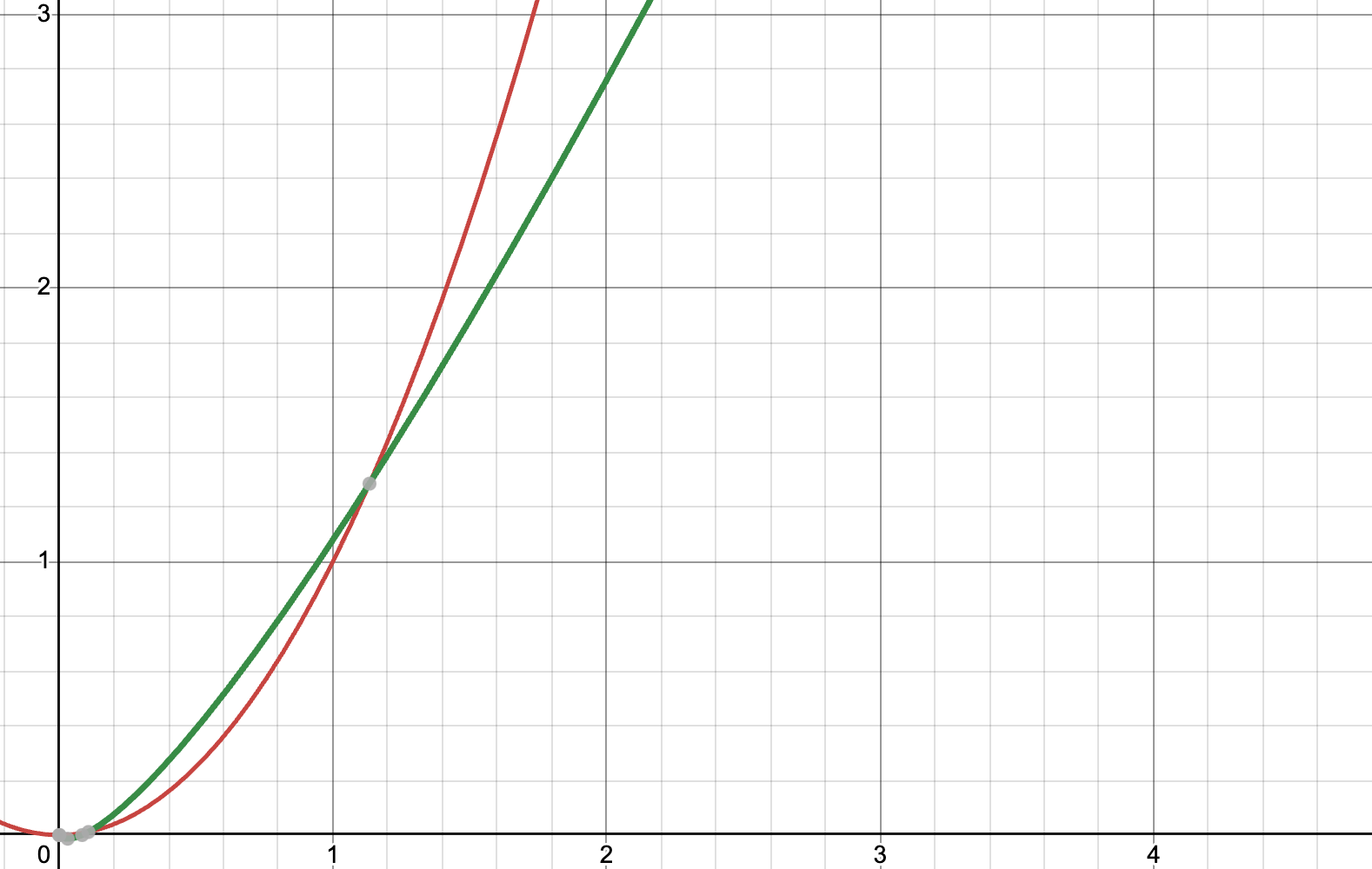
Esempio - l’algoritmo descritto dalla funzione rossa è asintoticamente più costoso ma per certi valori è conveniente rispetto all’algoritmo descritto dalla funzione verde.

Differenza tra complessità algoritmo e complessità del problema

Quando troviamo un algoritmo con complessità $O(g(n))$ per un problema, stiamo definendo una limitazione superiore (upper bound) alla complessità del problema.

Se si dimostra che qualunque algoritmo per quel problema ha complessità $\Omega (f(n))$, si è stabilita una limitazione inferiore (lower bound) alla complessità del problema.

Se $f(n)=g(n)$ allora l’algoritmo è detto ottimo, perché la sua complessità in ordine di grandezza risulta la migliore possibile.

Calcolare Limitazione Inferiore

Calcolare limitazioni inferiori significative ai problemi in genere non è un compito semplice. Sono noti pochi modi generali di dimostrazione per limitazioni inferiori.

Vediamone due molto semplici:

Dimensione dei Dati

Se un problema ha in ingresso n dati e richiede di esaminarli tutti, allora una limitazione inferiore della complessità è $\Omega (n)$.

Esempio - per il problema della ricerca del massimo in una lista, l’algoritmo banale che scorre la lista è ottimo.

Eventi Calcolabili

Se un problema richiede che un certo evento sia ripetuto almeno m volte, allora una limitazione inferiore della complessità è $\Omega (m)$.

Esempio - per gli algoritmi di ordinamento basati sul confronto si può dimostrare che se n sono gli interi da ordinare allora bisogna effettuare almeno $n\log n$ confronti e quindi $\Omega (n\log n)$ è il limite inferiore alla complessità e di conseguenza l’algoritmo heapsort è ottimo.

È raro sapere che un algoritmo è ottimo per un certo problema.

Problema Intrattabile

Un problema si dice intrattabile efficienti se non può avere algoritmi efficienti (polinomiali).