Valutazione del Tempo (MPI)

Le immagini e buona parte del testo di questa nota sono stati presi degli appunti di @CasuFrost.

---

Introduzione

Valutare il tempo di esecuzione di un programma multicore non è banale. La libreria MPI mette a disposizione la funzione double MPI_Wtime(), che restituisce il tempo trascorso a partire da un riferimento temporale arbitrario ma fisso durante l’esecuzione del programma.

Sebbene il valore restituito da una singola chiamata non sia particolarmente significativo, è possibile ottenere una misura utile valutando la differenza tra due chiamate a MPI_Wtime(). In questo modo si ottiene l’intervallo di tempo (elapsed time) tra i due istanti.

Tipicamente, si effettua una prima chiamata all’inizio e una seconda alla fine del programma. La differenza tra i due valori fornisce così il tempo di esecuzione del processo MPI.

double start_time = MPI_Wtime();
double finish;
 
/*codice*/
 
finish_time = MPI_Wtime();
printf("%lf", finish_time - start_time) ;

Problema 1 (processi con codice differente)

Problema: In un programma MPI, non è garantito che tutti i processi eseguano esattamente lo stesso codice o impieghino lo stesso tempo per completarlo. Ad esempio, ci potrebbero essere istruzioni condizionali del tipo if (rank == 0) {...} che fanno lavorare di più il processo di rank 0. Anche le operazioni collettive, come la costruzione di un albero di comunicazione, possono assegnare più lavoro ad alcuni nodi (es. il nodo radice) rispetto ad altri.

Questo significa che alcuni processi termineranno molto prima di altri, quindi il tempo di esecuzione totale del programma deve essere considerato come il massimo dei tempi impiegati dai singoli processi.

Soluzione: per ottenere il “vero” tempo totale di esecuzione del programma, si usano questi steps:

1. Ogni processo calcola localmente il proprio tempo di esecuzione con MPI_Wtime(), misurando l’istante di inizio e di fine
2. Si calcola la differenza tra i due tempi per ottenere il tempo locale di esecuzione
3. Si utilizza MPI_Reduce con l’operazione MPI_MAX per trovare il massimo fra tutti i tempi locali, che rappresenta il tempo totale di esecuzione

double local_start, local_finish, local_elapsed, elapsed; 
local_start = MPI_Wtime();
 
/* codice parallelo */
 
local_finish = MPI_Wtime(); 
local_elapsed = local_finish - local_start;
MPI_Reduce(&local_elapsed, &elapsed, 1, MPI_DOUBLE, MPI_MAX, 0, comm); 
 
if (my_rank == 0 ) {
	printf("%f\n", elapsed);
}

Problema 2 (esecuzione sfasata)

Problema: non è garantito che tutti i processi inizino a eseguire esattamente nello stesso istante. I tempi di avvio dei diversi rank possono essere leggermente sfasati, quindi se ogni processo registra il proprio tempo iniziale usando MPI_Wtime() in momenti diversi, la misura finale potrebbe risultare imprecisa rispetto all’effettiva durata del calcolo parallelo.

Soluzione: utilizzare MPI_Barrier per sincronizzare l’inizio

• La funzione collettiva MPI_Barrier(comm) forza tutti i processi a “fermarsi” e aspettare che anche gli altri raggiungano quel punto nel codice. Solo quando tutti sono arrivati, possono andare avanti. In questo modo, impostando il tempo di inizio subito dopo la MPI_Barrier, tutti i processi partono (quasi) dallo stesso stato di avanzamento, e la misura risulta più corretta.

Questo migliora la sincronizzazione, anche se non garantisce che i processi ripartano esattamente nello stesso istante, perché la MPI_Barrier stessa potrebbe usare strategie (come sincronizzazione in albero) che comportano piccoli sfasamenti residui. Tuttavia, per gli obbiettivi di questo corso questa approssimazione è più che accettabile.

Problema 3 (performance non deterministiche)

Problema: La misurazione del tempo impiegato da un processo è non deterministica, in quanto quest’ultimo è soggetto alle interruzioni del sistema operativo ed ai cambi di contesto, che possono variare in maniera apparentemente aleatoria. Nel caso in cui il programma venga eseguito in rete, tale rumore (il tempo casuale aggiunto all’esecuzione normale di un processo) è ancora maggiore.

Soluzione: Generalmente, è corretto eseguire più volte un processo misurando i tempi ad ogni esecuzione, per avere una misura statistica. Il minimo corrisponderà al caso ideale, il massimo al caso peggiore, la mediana al caso più frequente, è corretto fornire i dati di ogni esecuzione per avere un quadro chiaro dei tempi effettivi.

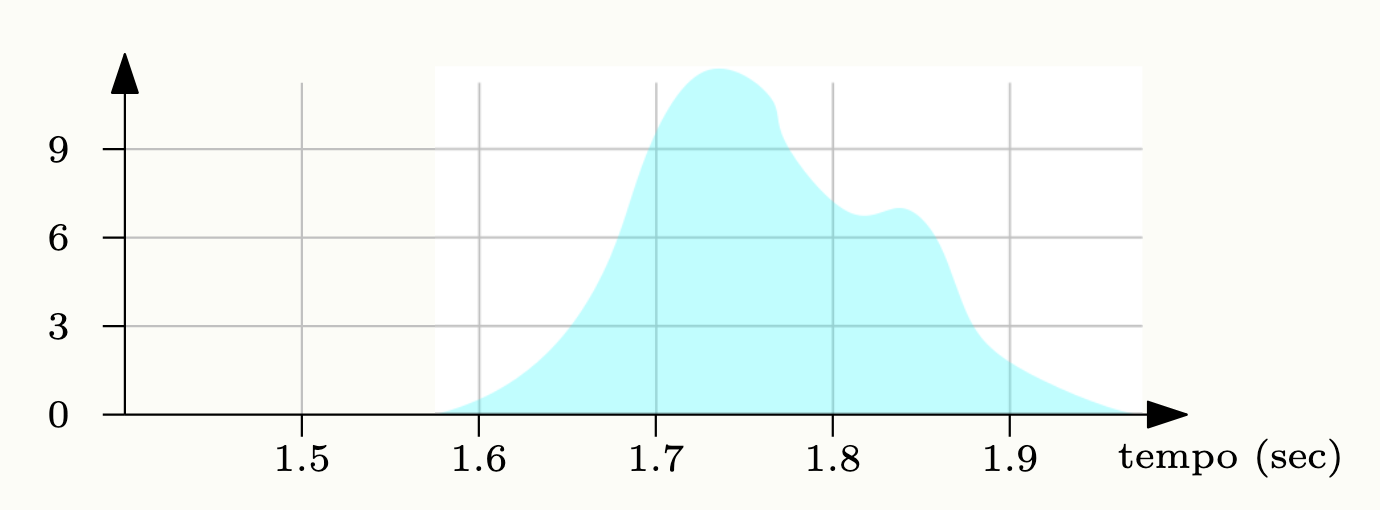
Misurazione Performance

Quindi per valutare il tempo di esecuzione dobbiamo:

1. Si mette una funzione barriera all’inizio dell’esecuzione
2. Si trova il massimo dei tempi di ogni processo
3. Si provano diverse esecuzioni ottenendo una distribuzione

Studio del Rumore, Speed-Up, Scalabilità ed Efficienza

Le interferenze ed i rumori sono stati grande oggetto di studio nella valutazione dei tempi, in particolare, si è osservato un rapporto di proporzionalità diretta fra il rumore ed il numero di processi impiegati in un calcolo, esiste quindi un limite, in cui l’aumento dei processi non garantisce un miglioramento dei tempi di esecuzione, bensì il contrario.

La seguente tabella, raccoglie i tempi di esecuzione in secondi di un algoritmo che esegue il prodotto fra matrici quadrate:

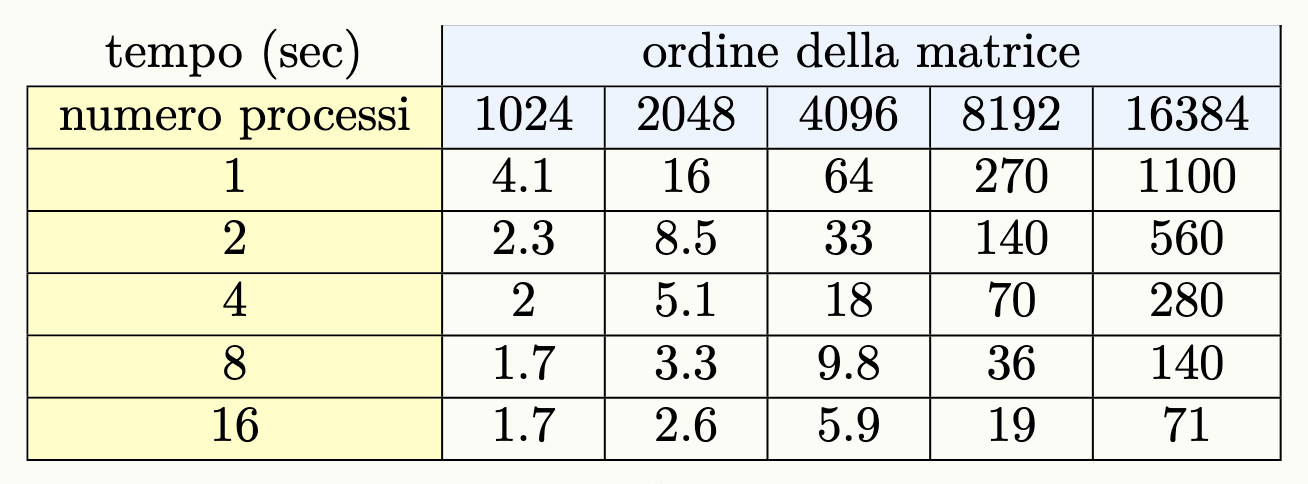
Per la stima dei tempi si definiscono le seguenti variabili:

• $T_s(n)$ è il tempo di esecuzione di un programma se eseguito in maniera sequenziale, con un input di dimensione n.
• $T_p(n,p)$ è il tempo di esecuzione di un programma se eseguito in maniera parallela con p processi, e con un input di dimensione n.

Speed-Up

Lo speed-up dell’applicazione misura il margine di miglioramento di un programma quando si esegue in parallelo piuttosto che in sequenziale:

$$S(n,p)=\frac{T_s(n)}{T_p(n,p)}$$

Nota: Ovviamente i tempi sequenziali e paralleli vanno misurati sullo stesso hardware.

L’ideale sarebbe uno speed up lineare (del tipo, $S(n,p)\simeq p$), nell’effettivo:

• l’aumentare dei processi fa diminuire lo speed-up
• l’aumentare dell’input lo fa aumentare lo speed-up

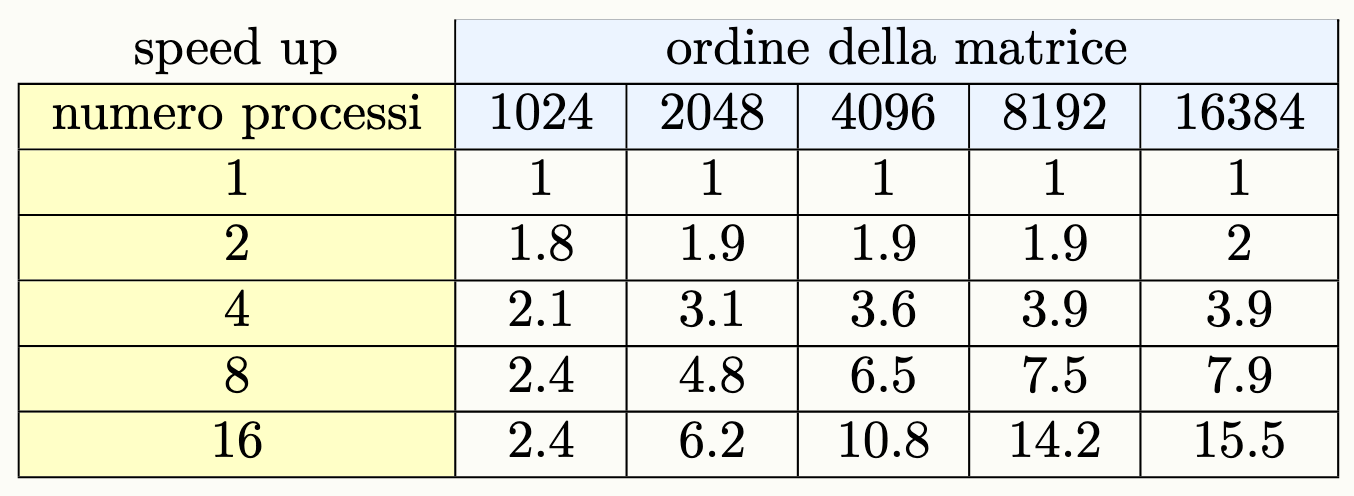
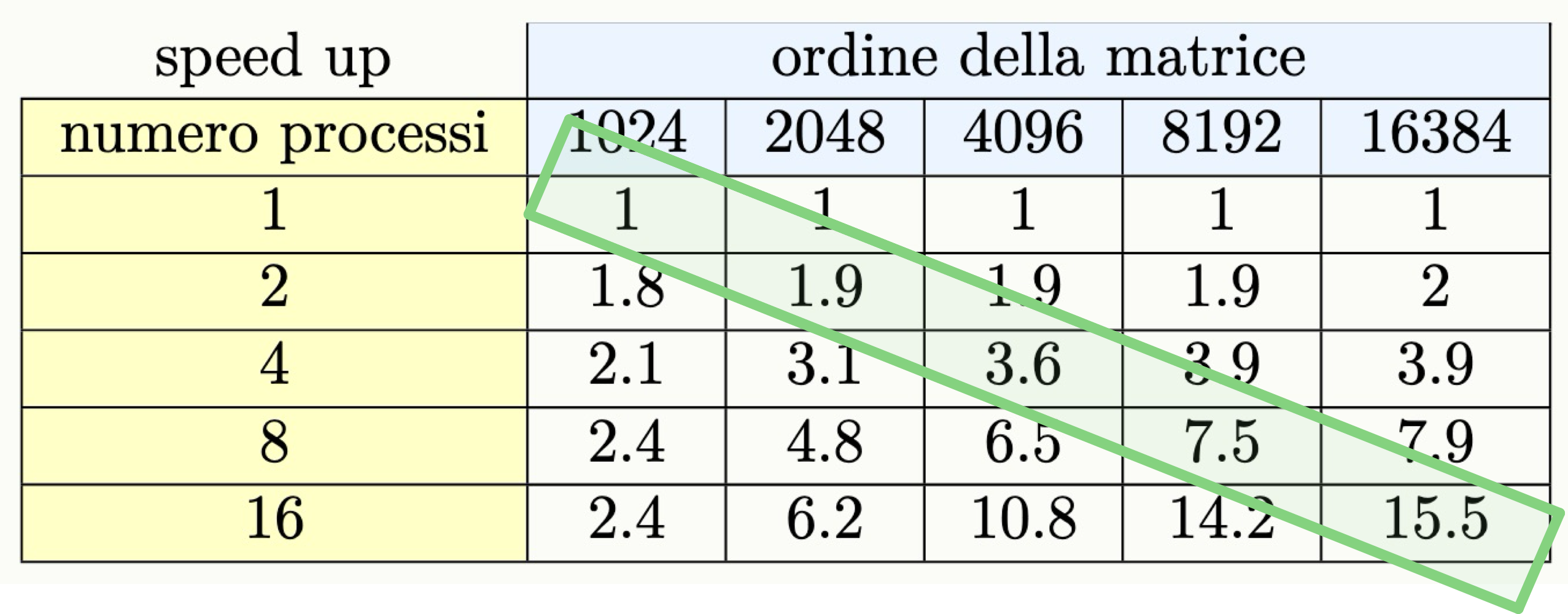
La seguente tabella riporta i valori dello speed-up del programma che esegue il prodotto fra matrici:

Nota: $T_p(n,1)\ne T_s(n)$, generalmente il tempo di esecuzione parallela con 1 processo è maggiore del tempo di esecuzione sequenziale (dato che il setup dell’ambiente per il calcolo parallelo ha un costo).

Scalabilità

La scalabilità di un processo è definita come segue:

$$S_c(n,p)=\frac{T_p(n,1)}{T_p(n,p)}$$

dove:

• $T_p(n,1)$ è il tempo che l’algoritmo impiega con 1 solo processo
• $T_p(n,p)$ è il tempo impiegato con p processi (a parità di input n)

Interpretazione: La scalabilità indica di quanto migliora (o peggiora) l’esecuzione del programma quando si aumenta il numero di processi, mantenendo fisso il problema da risolvere.

• Se $S_c(n,p)\approx p$, significa che aggiungere processi porta quasi a un’accelerazione proporzionale: il programma scala bene (scalabilità ideale).
• Se $S_c(n,p)<p$, la scalabilità reale è inferiore a quella ideale a causa di costi di comunicazione, sincronizzazione.

Un valore $S_c(n,p)<1$ indica che aggiungere processi peggiora il tempo, questo accade se i costi paralleli superano i benefici (ad esempio, per input troppo piccoli o rumori/overhead eccessivi).

Efficenza

L’efficienza invece è un valore compreso fra zero ed 1 definito come segue:

$$E(n,p)=\frac{T_p(n,1)}{p}=\frac{T_p(n,1)}{p\cdot T_p(n,p)}\in (0,1]$$

L’efficienza paragona lo speed-up ottenuto con il numero di processi:

• un valore di 1 significa uso perfetto delle risorse
• valori più bassi indicano sprechi dovuti all’overhead delle esecuzione parallela e alle comunicazioni.

Chiaramente, se le dimensioni dell’input sono piccole, l’utilizzo di tanti processi risulta inutile, l’efficienza è quindi bassa. L’utilizzo del multi processo ha senso quando l’input è di grande dimensione, in modo tale da ammortizzare il costo dell’overhead del parallelismo.

Scalabilità Forte e Scalabilità Debole

Prima di tutto dobbiamo tenere in considerazione che lo strong scaling e il weak scaling non sono uno l’opposto dell’altro, uno programma può essere sia week scalable che strongly scalable.

Un programma si dice strongly scalable se, data una dimensione fissa dell’input n, all’aumentare dei processi:

• lo speed up ha una buona crescita (ovvero l’efficienza rimane stabile)
• spesso un programma è strongly scalable solo per input sufficientemente grandi: lo stesso programma può non essere strongly scalable per un input n1 ma esserlo per un input più grande n2.

Un programma si dice weakly scalable se, all’aumentare dell’input, e all’aumentare del numero dei processi, il tempo di esecuzione varia di poco.

Si cerca lo weak scaling

Rendere un applicazione strongly scalable è estremamente difficile, per questo nell’effettivo viene considerato sempre il weak scaling quando si vuole parallelizzare un compito.

Esempio Strongly Scalable

Prendiamo un programma parallelo che esegue il prodotto tra matrici quadrate:

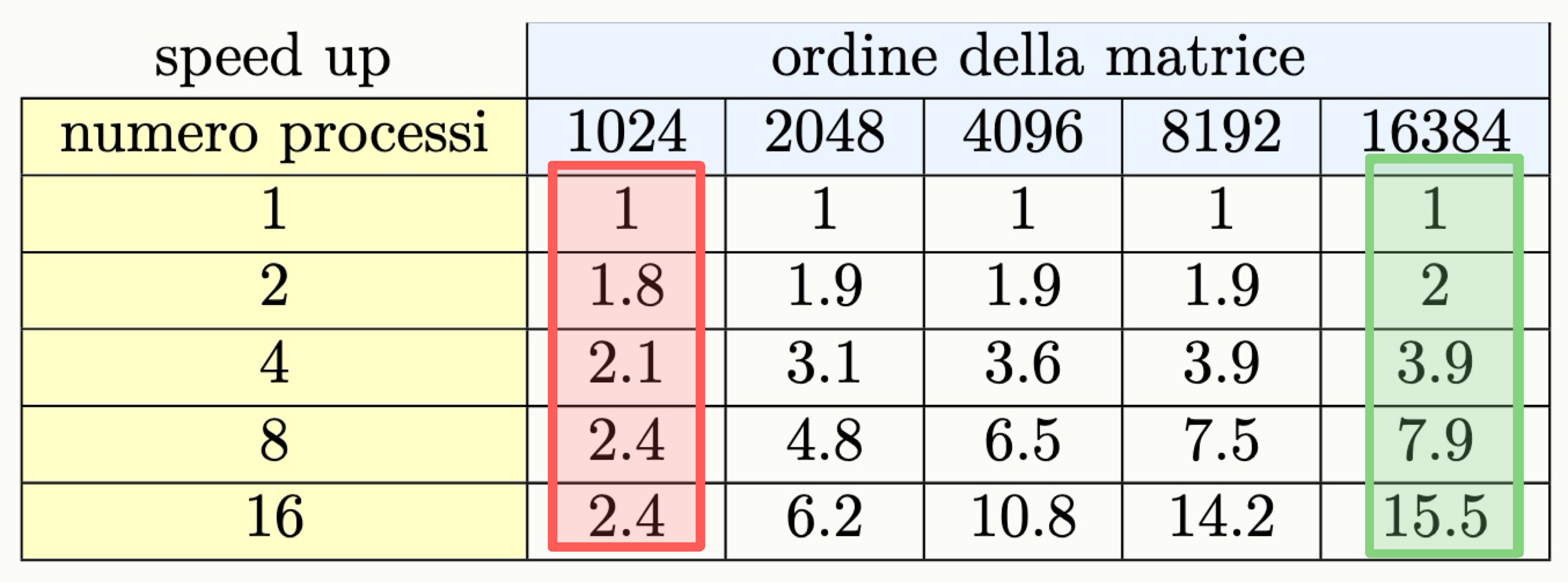
Come possiamo vedere il programma può essere considerato:

• not strongly scalable se n = 1024
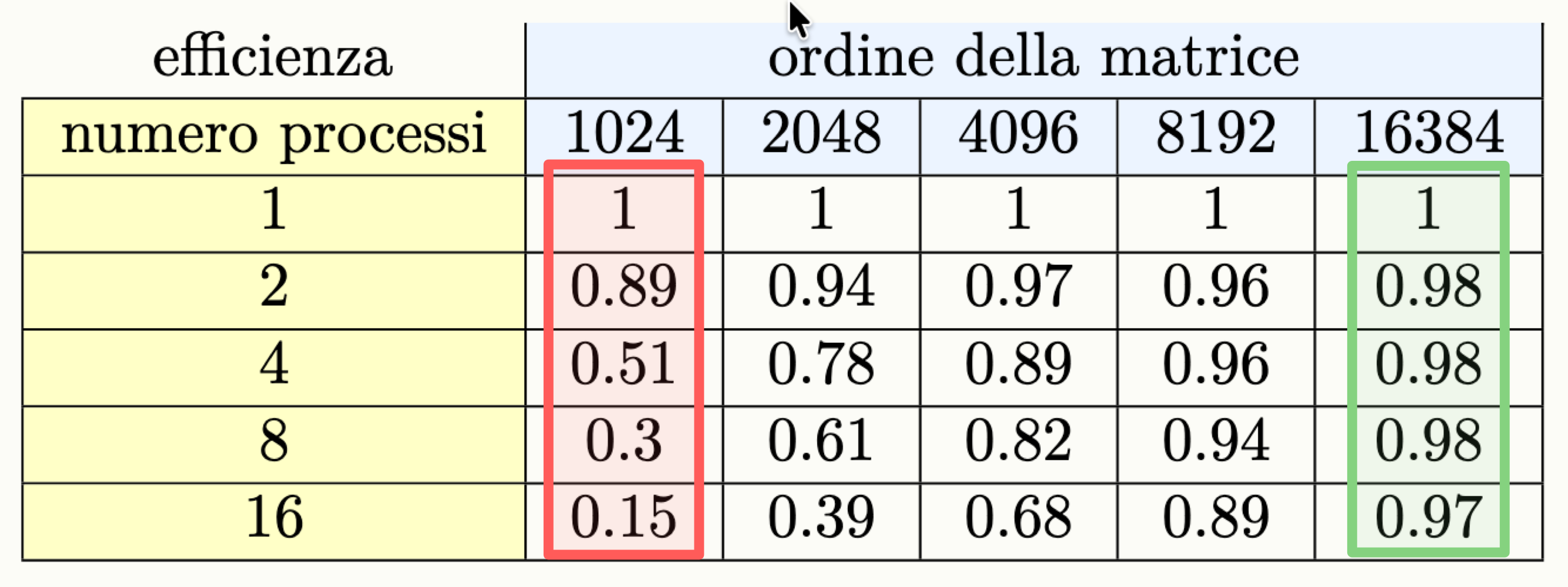
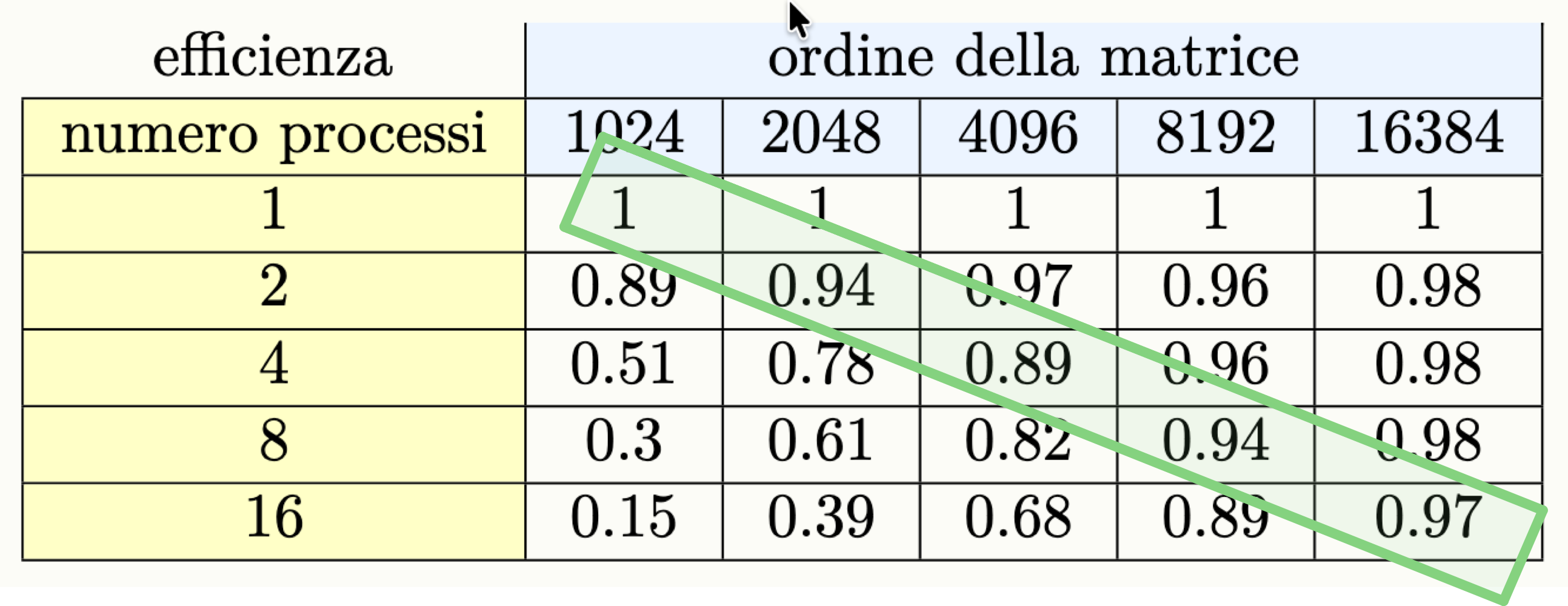
• strongly scalable se n = 16384

Questo è anche visibile guardando i dati sull’efficenza:

Esempio Weakly Scalable

Prendiamo lo stesso programma di prima, che esegue il prodotto tra matrici quadrate:

Come possiamo vedere il programma può essere considerato weakly scalable.

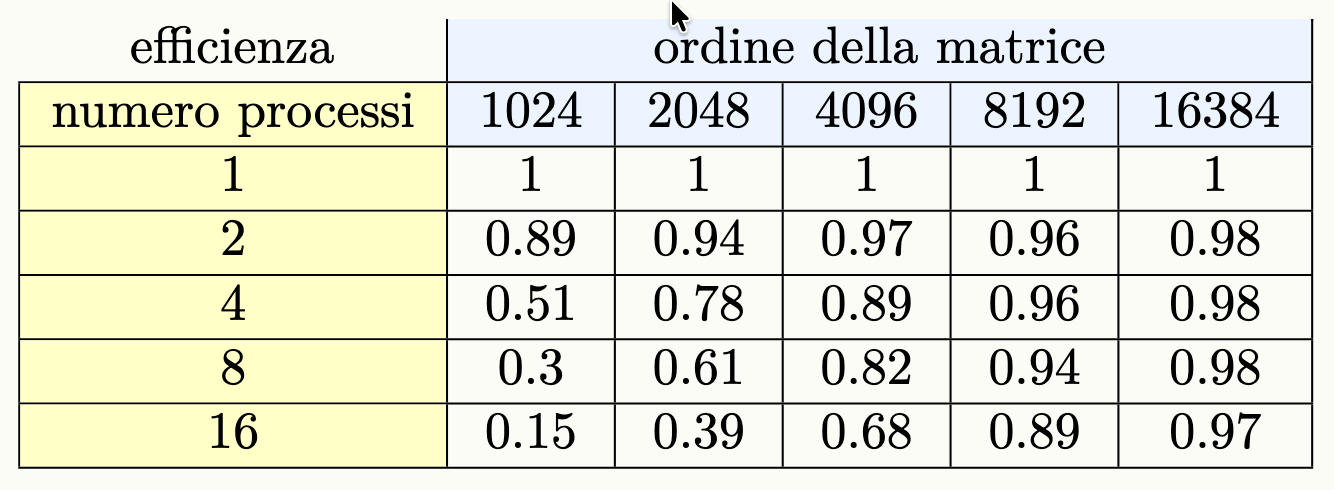
Lo stesso si può vedere studiano l’efficenza del programma.

Stimare la scalabilità di un programma (legge di Amdahl)

Dato un programma, si definisce frazione seriale la porzione di esso che è impossibile da parallelizzare, e viene espressa come un valore fra 0 ed 1.

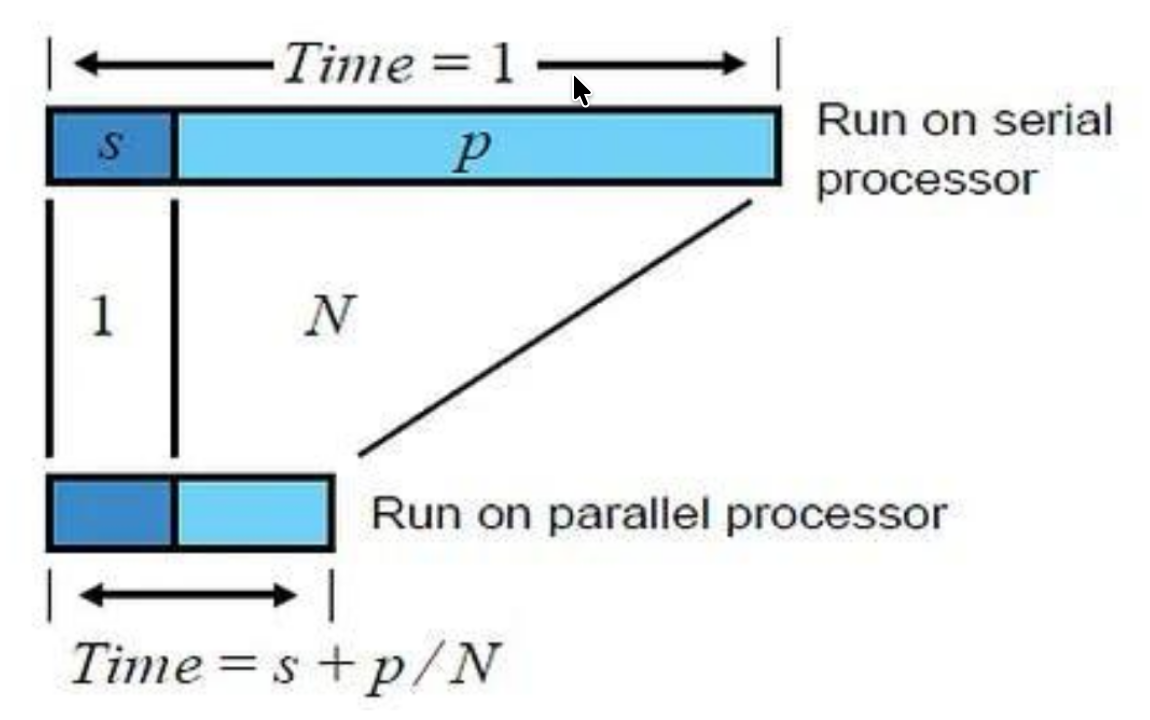
La parte seriale non potrà essere influenzata dalla parallelizzazione, la legge di Amdahl stabilisce che lo scaling di un’applicazione è limitato dalla frazione seriale.

Per un n dimensione in input fissata, si ha che il tempo di esecuzione parallela equivale a:

$$T_p(p)=T_s(1-\alpha )+\alpha \frac{T_s}{p}$$

Dove:

• $\alpha \in [0,1]$ rappresenta la frazione parallelizzabile
• $1-\alpha$ rappresenta la frazione seriale

Lo speed-up quindi è calcolabile attraverso:

$$S(p)=T_s\cdot \frac{1}{T_p(p)}=T_s\cdot \frac{1}{T_s(1-\alpha )+\alpha \frac{T_s}{p}}$$

Il valore dello speed up è limitato superiormente, infatti all’aumentare dei processi:

$$\begin{array}{rl}\underset{p\to \infty }{\lim }S(p)& =\underset{p\to \infty }{\lim }{T}_s\frac{1}{T_s(1-\alpha )+\alpha \frac{T_s}{p}}\\ & =\frac{T_s}{T_s(1-\alpha )}\\ & =\frac{1}{1-\alpha }\end{array}$$

Esempi

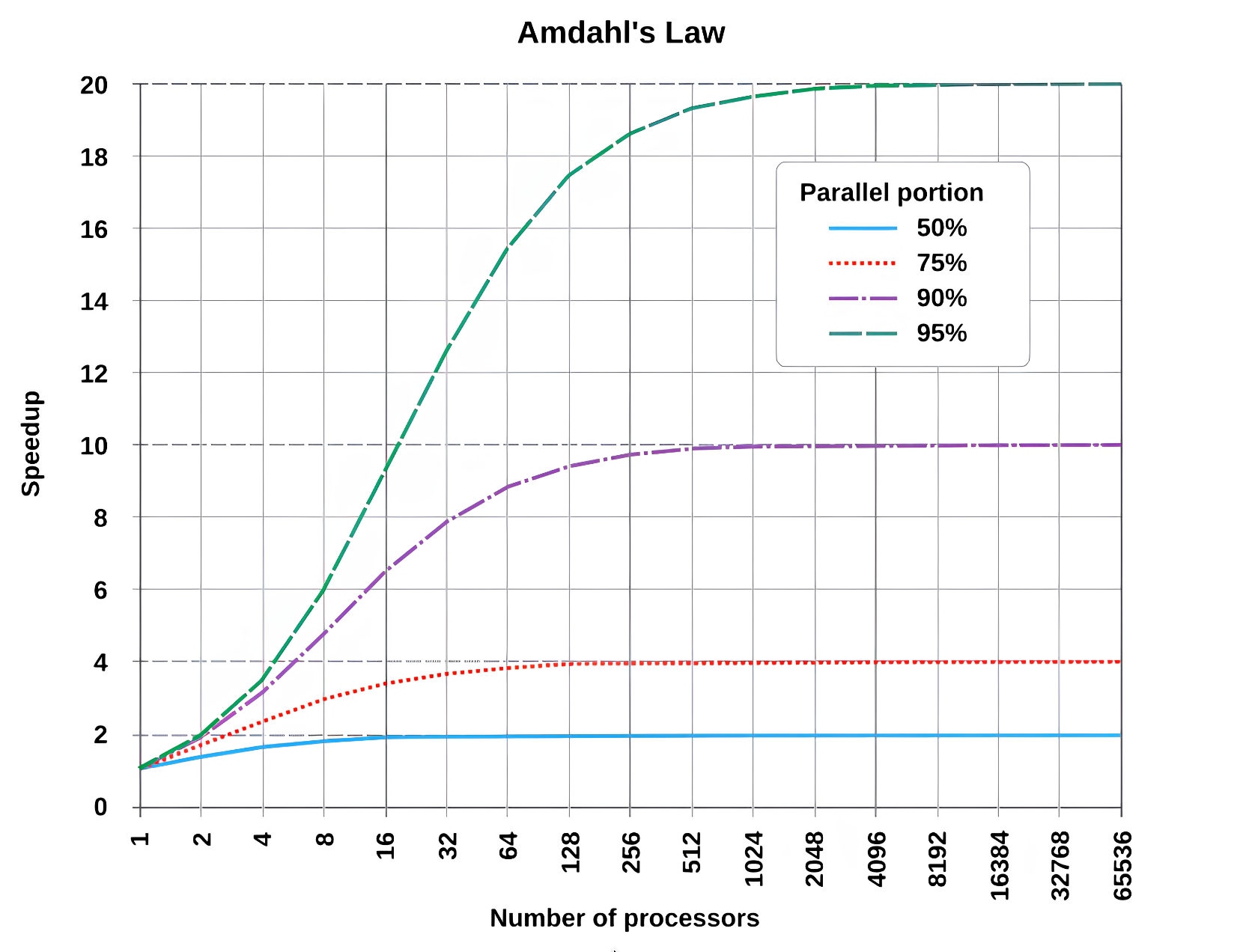
• Se il 50% del programma può essere parallelizzato ($\alpha =0.5$), il massimo speed-up teorico ottenibile è circa 2, anche usando molti processori.
• Se il 90% del programma può essere parallelizzato ($\alpha =0.9$), il massimo speed-up teorico ottenibile è 10.
• Per poter scalare fino a 100.000 processi, si deve avere una frazione parallelizzabile $\alpha \ge 0.99999$, cioè quasi tutto il programma deve essere parallelizzabile.

Strong Scaling

Naturalmente dato che studiando il programma con la legge di Amdahl dobbiamo tenere la dimensione (n) del problema fissa, significa che stiamo studiano lo strong scaling.

Per lo studio dello week scaling dobbiamo utilizzare la Legge di Gustafson.

Legge di Gustafson

La legge di Gustafson è definita ini questo modo:

$$S(n,p)=(1-\alpha )+\alpha p$$

Week Scaling

A differenza della legge di Amdahl, la legge di Gustafson tiene conto dello week scaling.

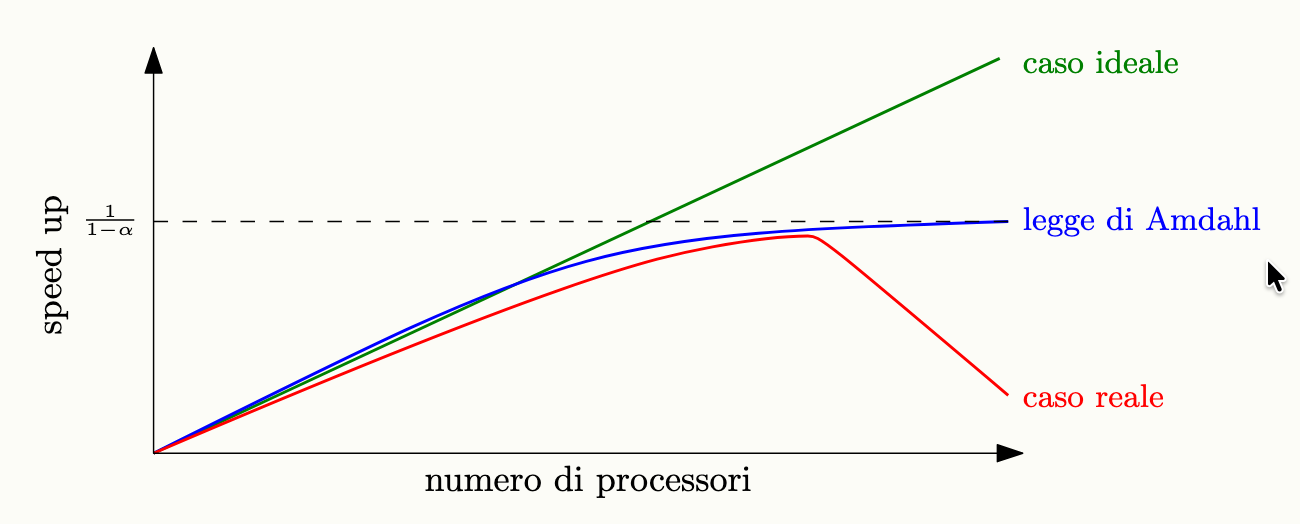
Mondo Reale

Nel caso reale, l’aumentare del numero di processi potrebbe far incrementare la frazione seriale.

Cosa sono i Thread

I core sono le unità di calcolo fisiche di un processore: ognuno esegue istruzioni in modo indipendente. I thread (o processori logici) sono unità di esecuzione virtuali ottenute tramite tecniche di multithreading (es. Hyper-Threading).

Nel caso di 8 core e 16 thread, ogni core può gestire contemporaneamente due thread diversi grazie a due “contesti di esecuzione” separati (registri, program counter, stack), ma le principali risorse hardware del core (ALU, cache L1) sono condivise tra i due thread.

Il vantaggio è che quando un thread è bloccato (ad esempio in attesa di dati), l’altro può utilizzare subito le unità di calcolo del core, migliorando l’efficienza in certe situazioni.