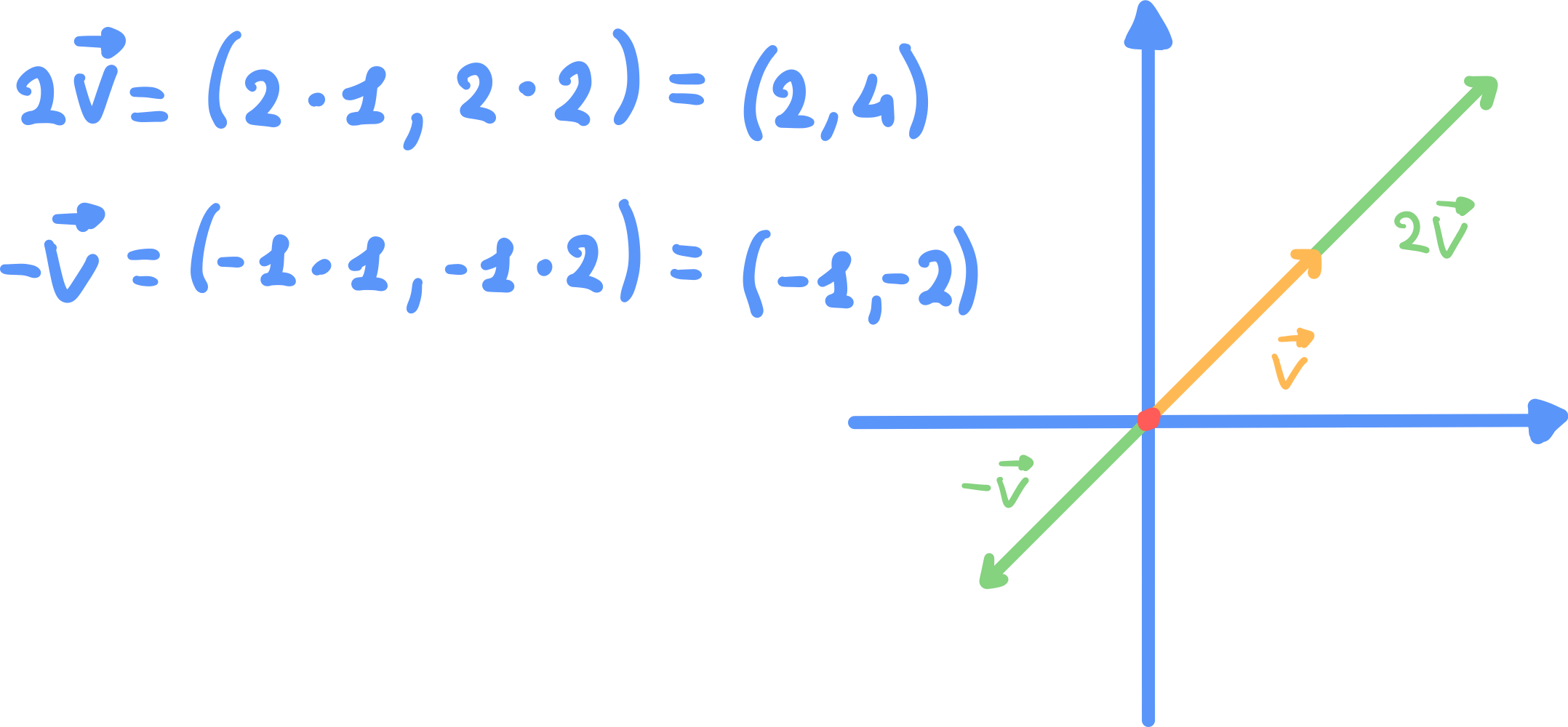Vettori nel Piano

Index

Related

---

Introduzione

Sistema di riferimento

• Quando si parla di vettori, prima di tutto, si deve esplicitare il sistema di riferimento.
• In questo caso parliamo di vettori nel piano cartesiano che a suo volta si può identificare con l’insieme ${\mathbb{R}}^2$ delle coppie ordinate di numeri reali.

Vettore

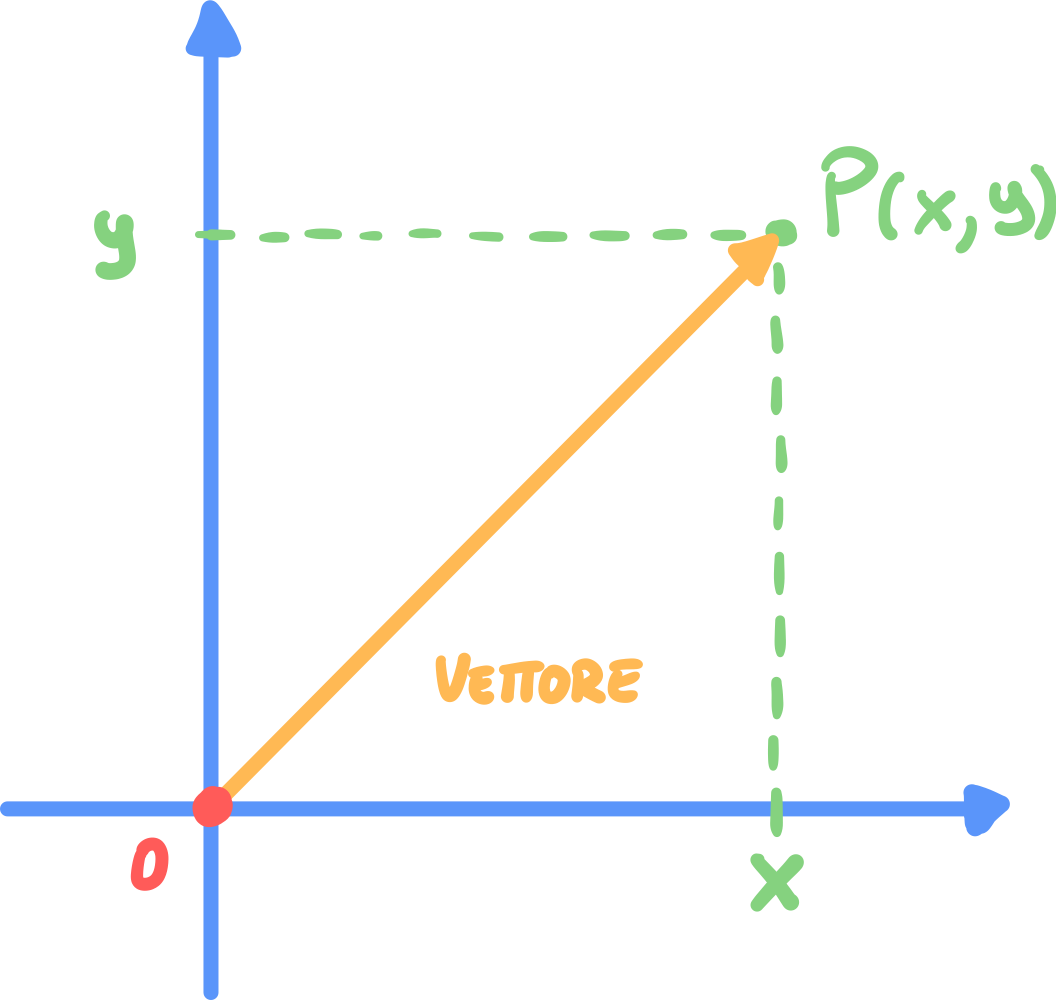
Ad ogni punto del piano cartesiano si può associare un vettore che possiamo pensare come un segmento orientato avete come estremi:

• L’origine del piano cartesiano
• Il punto stesso

---

Notazione

Per identificare il vettore $\vec{v}$ con la coppia ordinata $(x,y)$ delle coordinate del punto $p$, possiamo utilizzare;

$$\vec{v}=(x,y)$$

Dove $x$ e $y$ vengono chiamati componenti scalari.

Lunghezza del vettore

È possibile calcolare la lunghezza chiamata NORMA del vettore utilizzando il Teorema di Pitagora

$$|\vec{v}|=\sqrt{x^2+y^2}$$

---

Operazioni

Somma

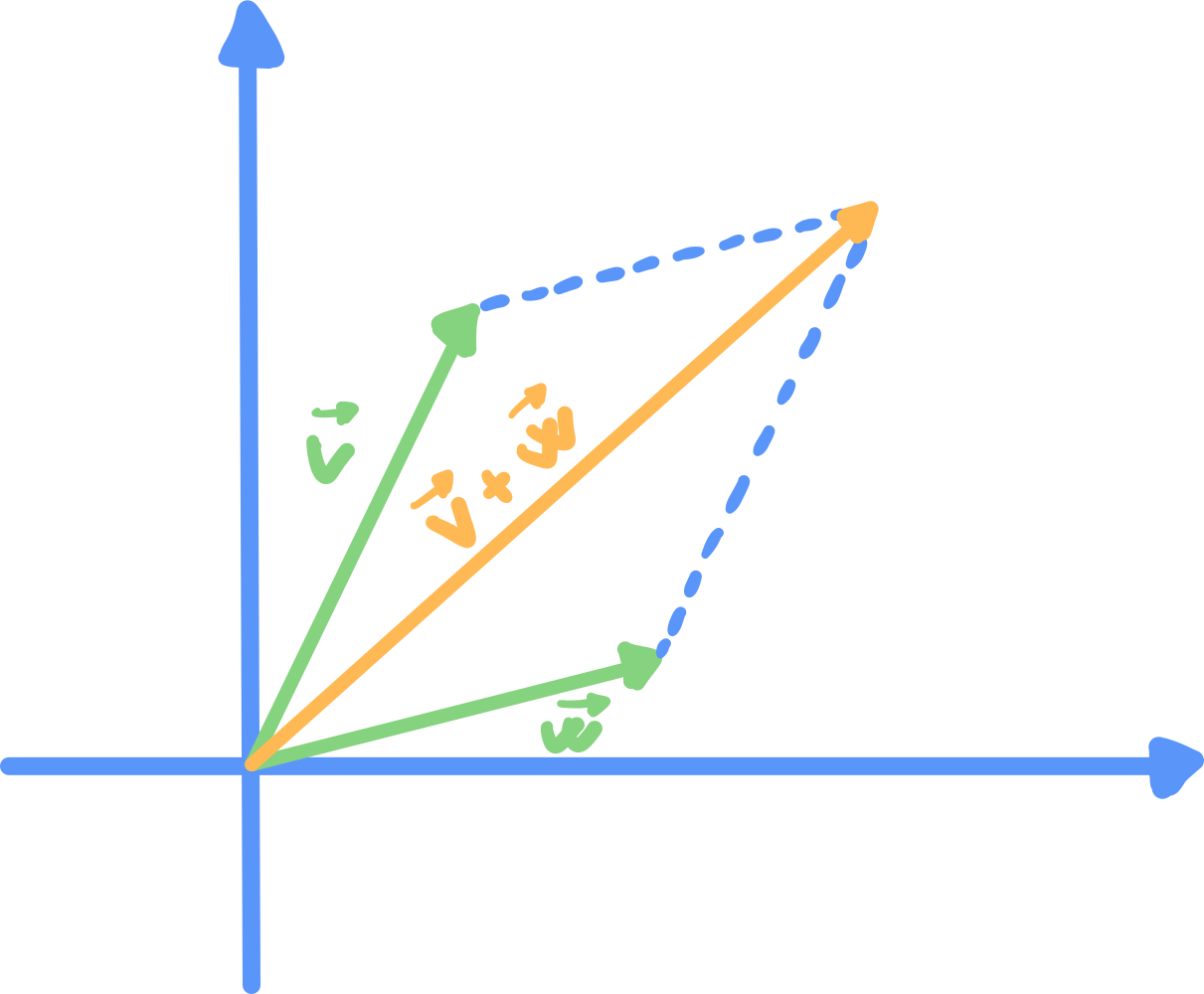
Dati due vettori $\vec{v}=(x_1,y_1)$ e $\vec{w}=(x_2,y_2)$, la somma tra $\vec{v}$ e $\vec{w}$ è un vettore avente per componenti la somma dei componendi dei due vettori:

$$\vec{v}+\vec{w}=(x_1+x_2,y_1+y_2)$$

Disuguaglianza Triangolare della Norma

$$|\vec{v}+\vec{w}|\le |\vec{v}|+|\vec{w}|$$

oss: questo non vale se i due vettori sono paralleli e hanno lo stesso verso\

Moltiplicazione

Dato il vettore $\overrightarrow{v=(x,y)}$ ed il numero reale $\lambda$. Il vettore $\lambda \cdot \vec{v}$ ha per componenti le componenti del vettore $\vec{v}$ moltiplicate per $\lambda$.

$$\lambda \vec{v}=(\lambda x,\lambda y)$$

Esempio

Norma del vettore risultante $\lambda$ con segno positivo:

$$|\vec{v}k|=|\vec{v}|\cdot |k|$$