Albero BFS

Introduzione

La visita in ampiezza (BFS) può generare un albero detto albero BFS, che rappresenta i cammini minimi per tutti i nodi raggiungibili partendo da un nodo iniziale s.

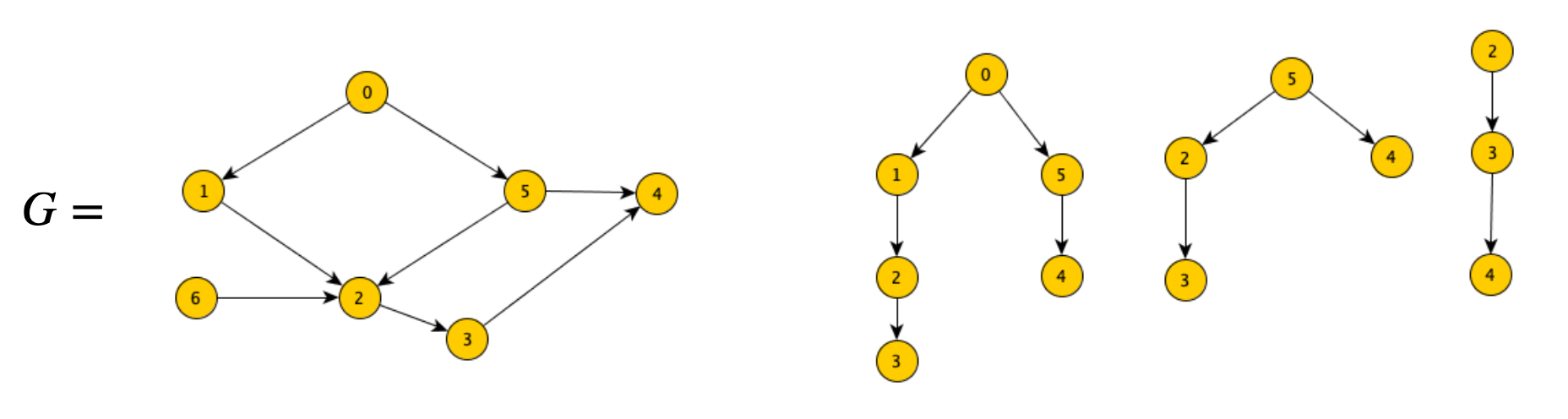
Proprietà

La distanza minima di un vertice x dalla sorgente s nel grafo G equivale alla profondità di x nell’albero BFS.

Algoritmo Vettore dei Padri

Calcoliamo il vettore dei padri del albero BFS in $O(n+m)$.

def BFSpadri(x, G) :
	'''
	Restituisce l'albero BFS radicato in `x` rappresentato
	attraverso un vettore dei padri
	'''
	
	P = [-1] * len(G)
	P[x] = x    # radice
	
	testa = 0
	while len(coda) > testa:
		u = coda[i]
		i += 1
		for y in G[u]:
			if P[y] == -1:
				P[y] = u
				coda.append(y)
	return P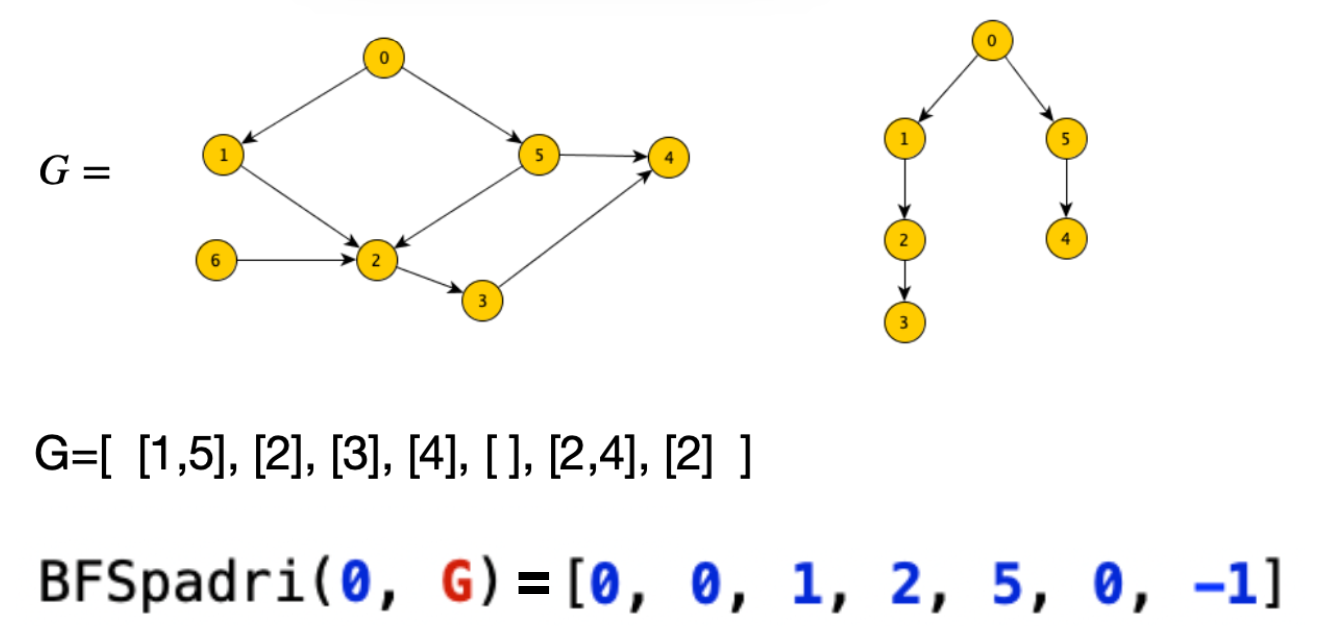

Algoritmo Vettore delle Distanze

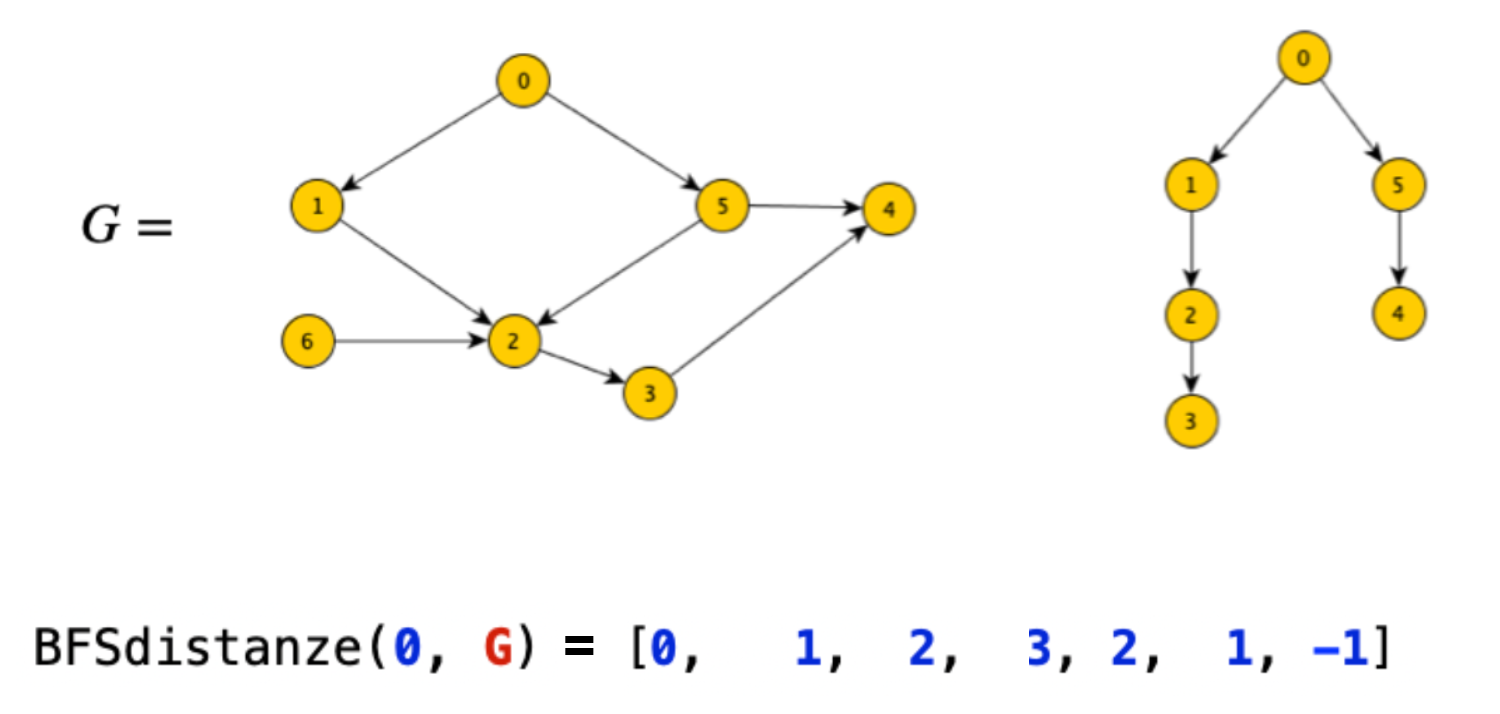
Il vettore delle distanze D di un grafo è un vettore i cui elemento D[x] rappresenta la distanza del nodo x dal nodo sorgente s.

É possibile determinare questo vettore in $O(n+m)$ modificando leggermente la procedura di visita vita precedentemente.

def BFSdistanze(x,G):
	'''
	Restituisce il vettore delle distanze da `x` in `G`
	'''
	
	D = [-1] * len(G)
	D[x] = x    # radice
	
	testa = 0
	while len(coda) > testa:
		u = coda[i]
		i += 1
		for y in G[u]:
			if P[y] == -1:
				D[y] = D[u] + 1
				coda.append(y)
	return D