Visita in Ampiezza (BFS) - Grafi

Introduzione

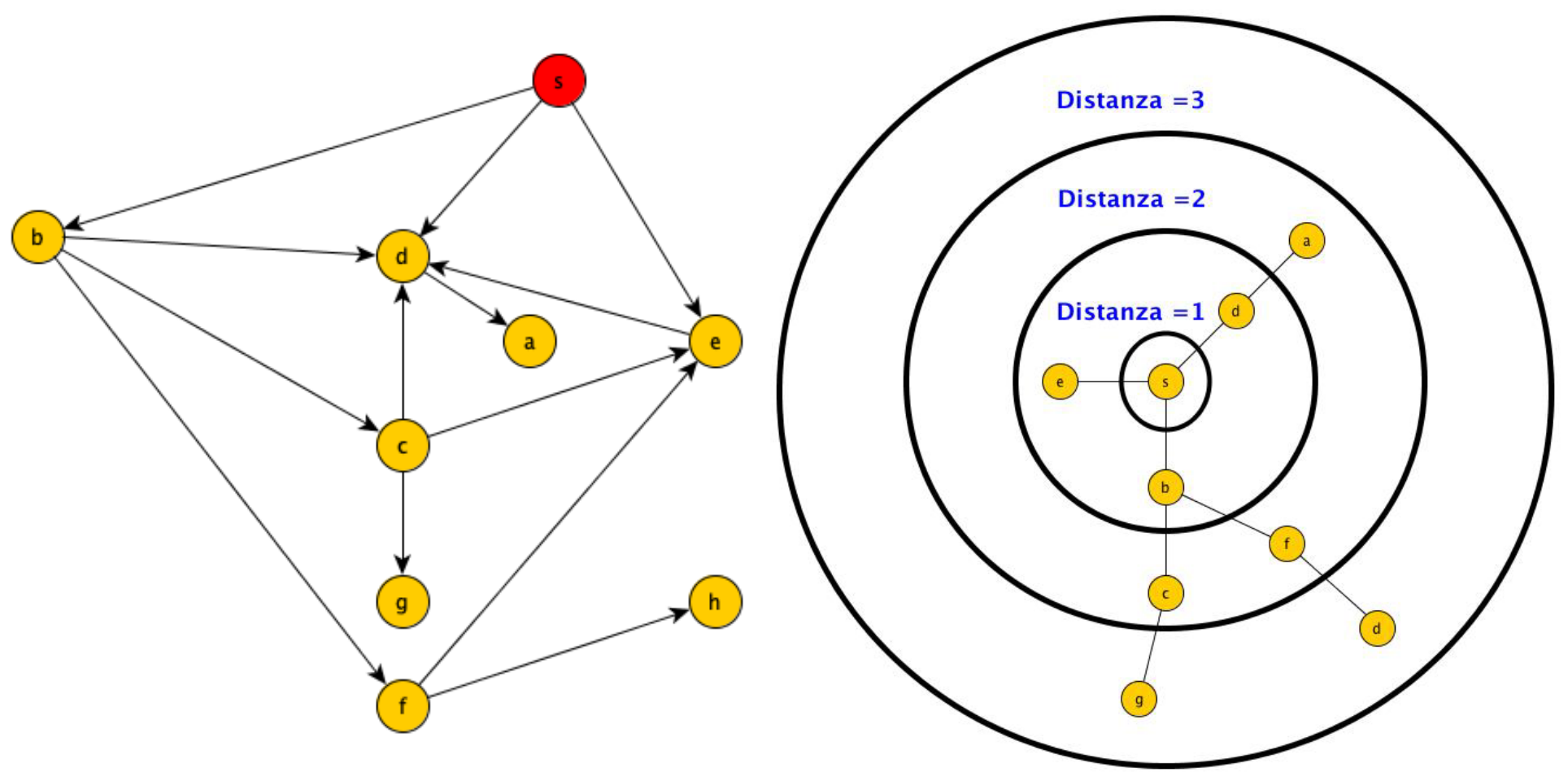
La visita in ampiezza (Breadth First Search) esplora i nodi del grafo partendo da quelli a distanza 1 dal nodo iniziale x. Poi visita quelli a distanza 2 e così via.

oss: L’algoritmo visita tutti i vertici a livello k prima di passare a quelli a livello k+1.

Definizione Distanza

Dati due nodi a e b di un grafo G, definiamo la distanza tra a e b in G come il numero minimo di archi da attraversare per raggiungere b partendo da a.

Se il nodo b non è raggiungibile partendo da a allora la loro distanza è posta a $+\infty$.

Algoritmo

Per effettuare questo tipo di visita manteniamo in una coda i nodi visitati i cui adiacenti non sono stati ancora esaminati.

Ad ogni passo, preleviamo il primo nodo dalla coda, esaminiamo i suoi adiacenti e se scopriamo un nuovo nodo lo visitiamo e lo aggiungiamo alla coda.

Ricerca Nodi Raggiungibili

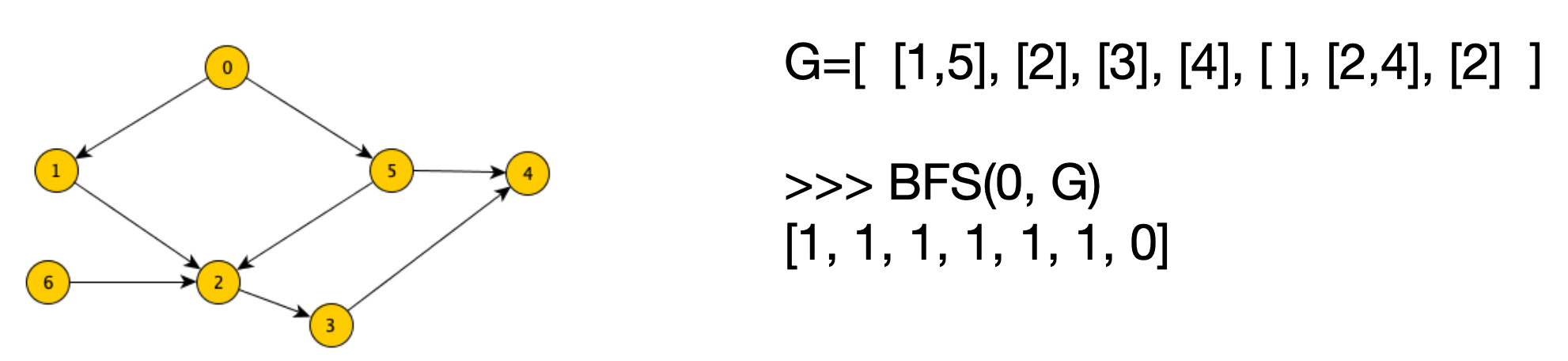
Applichiamo la BFS per ottenere i nodi raggiungibili a partire da un fissato nodo x.

Si comincia con una coda contenente il solo nodo di partenza x, fino a che la coda non risulta vuota, ad ogni passo:

• Un nodo viene estratto dalla coda
• Tutti i suoi adiacenti vengono visitati e messi in coda

def BFS(x, G):
	'''
	restituisce i nodi raggiungibili da `x` in `G`.
	'''
	visitati = [0]*len(G)
	visitati[x] = 1
	
	coda = [x]
	while coda:       
		u = coda.pop(0)
		for y in G[u]:
			if visitati[y] == 0:
				visitatu [y] = 1
				coda.append(y)
	return visitati

Problema: coda.pop(0) può richiedere $O(n)$ e visto che il while verrà eseguito $O(n)$ volte (tutti i nodi raggiungibili da x) in totale il costo computazionale di questa applicazione è $O(n^2)$.

Soluzione: Questo applicazione pò essere implementa con un costo di $O(n+m)$, se invece di effettuare pop(0) utilizziamo delle cancellazioni logiche.

Quindi utilizziamo un puntatore testa per indicare l’inizio della coda all’interno della lista, ed incrementando il puntatore di 1 possiamo “eliminare” a livello logico il primo elemento della coda, ricreando la funzionalità del pop(0) ma in costo $\Theta (1)$.

def BFS(x, G):
	'''
	restituisce i nodi raggiungibili da `x` in `G`.
	'''
	visitati = [0]*len(G)
	visitati[x] = 1
	
	coda = [x]
	testa = 0
 
	while len(coda) > testa:       
		u = coda[i]
		i += 1
		for y in G[u]:
			if visitati[y] == 0:
				visitatu [y] = 1
				coda.append(y)
	
	return visitati

Output

Ritorna il vettore visitati dove visitati[u] = 1 se e solo se u è raggiungibile da x.

Costo Coputazionale

Questa versione ha come costo temporale $O(m+n)$.