Introduzione
Si consideri adesso il seguente esempio, si vuole scrivere un programma che esegua l’integrazione numerica di una generica funzione f(x) (in queste esempio usiamo il coseno) tramite la regola del trapezoide.
Tale metodo consiste nel dividere l’intervallo di integrazione in n intervalli uguali:
lunghi h, di cui verrà calcolata l’area approssimandola ad un trapezio.
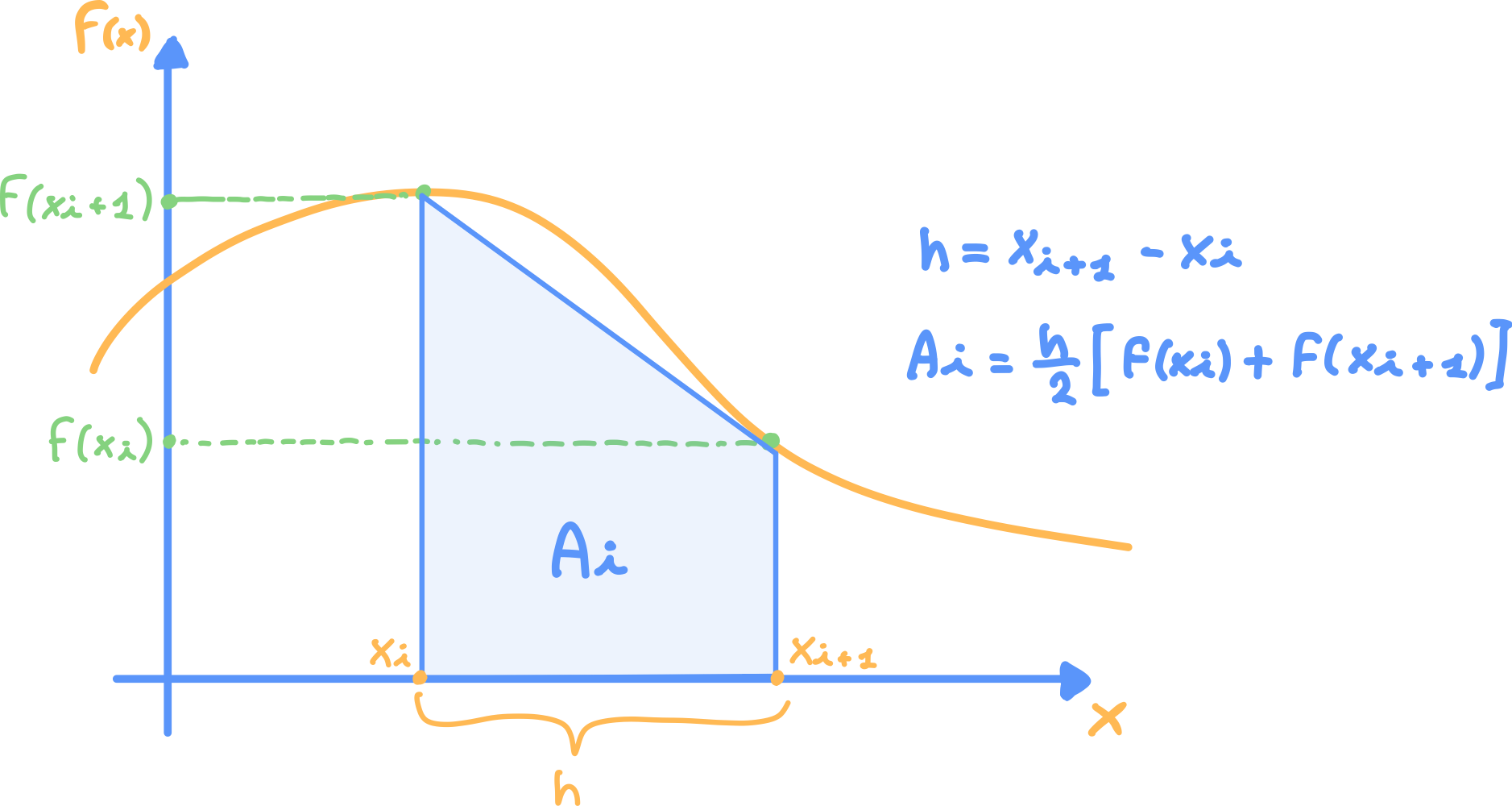
L’integrale approssimato sarà la somma totale di tutti i trapezoidi:
Versione Seriale
Prima di tutto implementiamo una versione seriale, in modo tale da studiare il problema e poi riutilizzare/riadattare la soluzione per la versione multicore.
#include <stdio.h>
#include <math.h>
double Integrale_Seriale(double a, double b, int num_seg) {
//a: estremo sinistro di integrazione
//b: estremo destro di integrazione
//num_seg: numero di segmenti (più è alto minore è l'approssimazione)
double h = (b-a)/num_seg; //altezza di ogni segmento
double area, local_a, local_b;
for (int i=0; i<num_seg; i++) {
local_a = a + i*h;
local_b = local_a + h;
area += h/2 * (cos(local_a)+cos(local_b));
}
return area;
}Quindi questo programma applica le formule viste nell’Introduzione per calcolare l’integrale dal punto a al punto b della funzione, approssimandolo effettuando il calcolo num_seg trapezoidi.
Versione Multicore
L’idea è quella di far eseguire la versione seriale del programma su più core, dove ognuno di questi calcola l’integrale su una sotto-parte della parte di funzione presa in analisi, e alla fine dei calcoli unire tutti i risultati.
Una prima versione di questo programma è:
#include <stdio.h>
#include <math.h>
#include <mpi.h>
int main(void) {
//calcoliamo l'integrale della funzione coseno da 0 a 1
int n_seg = 1000; // numero di segmenti, più è grande, più la stima sarà precisa
double a = 0.0; // estremo sinistro di integrazione
double b = 1.0; // estremo destro di integrazione
double h = (b-a)/n_seg; // altezza dei segmenti
double local_a, local_b;
double local_sum, total_sum;
int local_n_seg;
int my_rank, comn_size;
MPI_Init(NULL,NULL);
MPI_Comm_rank(MPI_COMM_WORLD, &my_rank);
MPI_Comm_size(MPI_COMM_WORLD, &comn_size);
local_n_seg = n_seg/comn_size; // numero di segmenti per ogni processo
local_a = a + (h * local_n_seg * my_rank);
local_b = local_a + (h * local_n_seg);
local_sum = Integrale_Coseno_Seriale(local_a, local_b, local_n_seg);
if (my_rank != 0) {
// invio della somma parziale al processo con rank 0
MPI_Send(&local_sum, 1, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD);
} else {
total_sum = local_sum;
for (int source = 1; source<comn_size; source++) {
MPI_Recv(&local_sum, 1, MPI_DOUBLE, source, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
total_sum += local_sum;
}
printf("Con n = %d trapezoidi, il calcolo dell'integrale approssimato della funzione coseno da %f a %f è %f\n",
n_seg, a, b, total_sum);
}
MPI_Finalize();
return 0;
}
double Integrale_Coseno_Seriale(double a, double b, int num_seg) {
//a: estremo sinistro di integrazione
//b: estremo destro di integrazione
//num_seg: numero di segmenti (più è basso maggiore è l'approssimazione)
double h = (b-a)/num_seg; //altezza di ogni segmento
double area, local_a, local_b;
for (int i=0; i<num_seg; i++) {
local_a = a + i*h;
local_b = local_a + h;
area += h/2 * (cos(local_a)+cos(local_b));
}
return area;
}MPI_Reduce
Se riprendiamo la prima versione dell’esempio del calcolo dell’integrale utilizzando MPI è possibile notare che il processo di rank zero ha un carico di lavoro superiore rispetto ogni altro processo, infatti, quest’ultimo oltre la somma dei suoi trapezi locali, deve calcolare la somma totale, inoltre deve occuparsi di ricevere i dati da tutti gli altri processi.
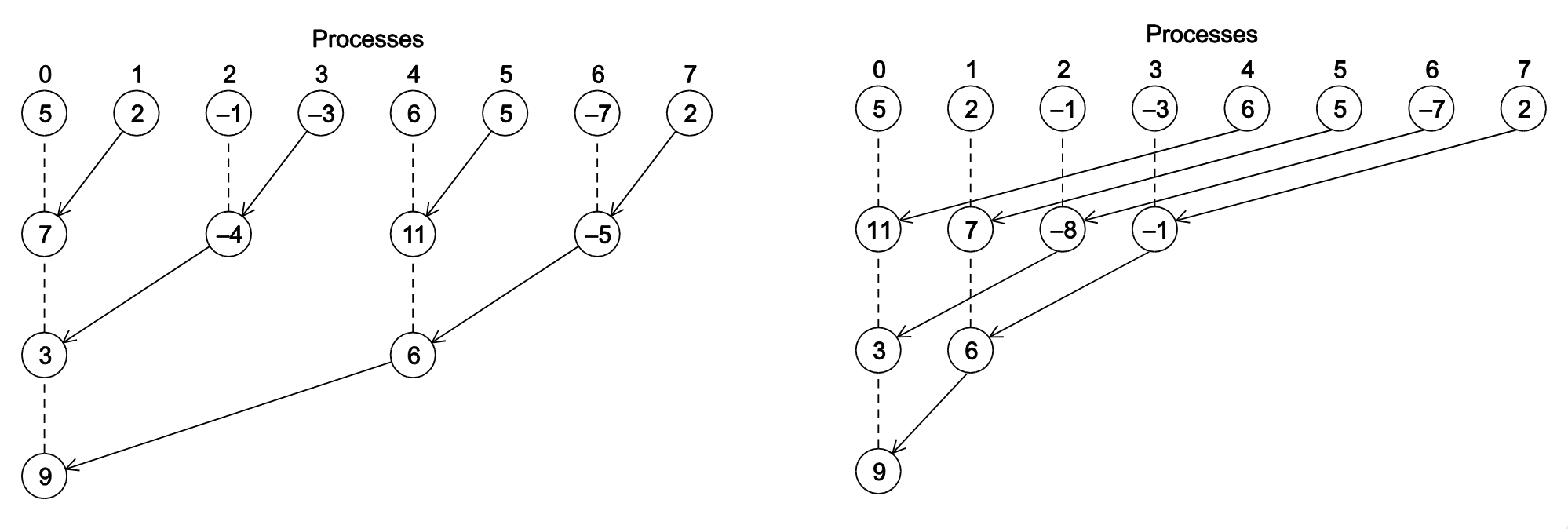
Una possibile soluzione consiste nel suddividere il carico utilizzando una struttura ad albero, così che il lavoro aggiuntivo dovuto alla comunicazione e all’aggregazione dei dati parziali risulti distribuito in modo logaritmico rispetto al numero dei processi coinvolti.
Esempi strutture a l’albero
oss: sono tutte e due soluzioni valide, ottimalità di una soluzione piuttosto che di un altra può dipendere da diversi fattori non sempre analizzabili, come la topologia fisica della rete attraverso cui sono collegate le macchine che eseguono i processi.
Ma utilizzando MPI non dobbiamo preoccuparci di implementare ogni volta un codice che suddivide il carico della riduzione su più nodi, infatti esiste la chiamata collettiva MPI_Reduce che in automatico sceglierà l’algoritmo migliore per suddividere il carico della aggregazione dei dati parziali.
Quindi possiamo semplificare e ottimizzare il codice utilizzando MPI_REDUCE invece di MPI_send e MPI_Recv:
#include <stdio.h>
#include <math.h>
#include <mpi.h>
double Integrale_Coseno_Seriale(double a, double n, int num_seg);
int main(void) {
//calcoliamo l'integrale della funzione coseno da 0 a 1
int n_seg = 1000; // numero di segmenti, più è grande, più la stima sarà precisa
double a = 0.0; // estremo sinistro di integrazione
double b = 1.0; // estremo destro di integrazione
double h = (b-a)/n_seg; // altezza dei segmenti
double local_a, local_b;
double local_sum, total_sum;
int local_n_seg;
int my_rank, comn_size;
MPI_Init(NULL,NULL);
MPI_Comm_rank(MPI_COMM_WORLD, &my_rank);
MPI_Comm_size(MPI_COMM_WORLD, &comn_size);
local_n_seg = n_seg/comn_size; // numero di segmenti per ogni processo
local_a = a + (h * local_n_seg * my_rank);
local_b = local_a + (h * local_n_seg);
local_sum = Integrale_Coseno_Seriale(local_a, local_b, local_n_seg);
MPI_Reduce(&local_sum, &total_sum, 1, MPI_DOUBLE, MPI_SUM, 0, MPI_COMM_WORLD);
if (my_rank == 0) {
printf("con n = %d trapezoidi, il calcolo dell'integrale approssimato della funzione coseno da %f a %f è %f\n",
n_seg, a, b, total_sum);
}
MPI_Finalize();
return 0;
}