File B-tree

Introduzione

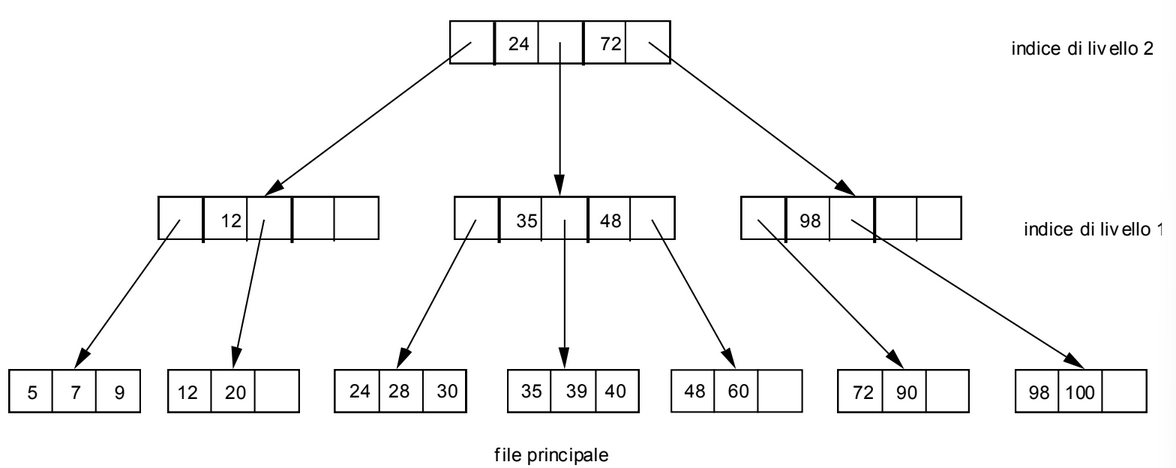
Il B-Tree è una generalizzazione del File con Indice dove non è presente un solo indice ma una gerarchia di indici.

L’indice a livello più alto è chiamato radice ed è costituito da un singolo blocco, che risiede in memoria principale durante l’utilizzo del file.

Importante: Ogni blocco di un B-Tree, sia indice che file principale, deve essere pieno almeno per metà, tranne eventualmente la radice.

Struttura

Ogni blocco di un file indice è costituito da record contenenti una coppia (v, b), dove:

• v è il valore della chiave del primo record della porzione di file principale accessibile attraverso il puntatore b.
• b è il puntatore che può puntare ad un blocco del file indice a livello immediatamente più basso o ad un blocco del file principale.

Ottimizzazione dello spazio:

• In ogni blocco del file indice possiamo risparmiare spazio memorizzando, per il primo record, soltanto il puntatore.
• Non ci serve sapere il valore più basso che troveremo, poiché se dobbiamo cercare un valore più piccolo di quello presente nel secondo record, lo andremo a cercare sicuramente nel primo.

Esempio

---

Ricerca

Per cercare un record con un dato valore, si accede agli indice di livello più alto e si scende nei livelli più bassi, restringendo la porzione del file principale in cui potrebbe trovarsi il record in un unico blocco.

1. Si parte dalla radice e si esaminano i blocchi uno per uno.
2. Se il blocco esaminato è un blocco del file principale, allora quello è il blocco in cui potrebbe trovarsi il record.
3. Se invece è un blocco del file indice, si cerca in quel blocco un valore della chiave che ricopre il valore che stiamo cercando e poi si segue il puntatore associato a quel valore, proseguendo così in un altro livello.

Costo della ricerca: La ricerca richiede h+1 accessi a memoria, dove h è l’altezza dell’albero e 1 è l’acceso ad un blocco del file principale.

Osservazioni

• Più i blocchi sono pieni, più sarà piccolo h e quindi meno costerà la nostra ricerca. Per questo motivo, chiediamo che i blocchi siano pieni almeno per metà.
• Tuttavia, se i blocchi sono completamente pieni, un inserimento può richiedere una modifica dell’indice ad ogni livello e in alcuni casi far crescere l’altezza di un livello.

---

Inserimento

L’inserimento di un nuovo record all’interno del file principale inizia con la ricerca del blocco in cui inserire il record (costo h+1).

Una volta trovato il blocco in procedimento dipende dal fatto se è presente spazio nel blocco oppure no:

Se il blocco non è pieno, allora:

• Possiamo aggiungere il nuovo record all’interno del record
• Costo +1 per riscrivere il blocco con un record aggiuntivo

Se il blocco è pieno, allora:

• Dobbiamo “sdoppiare” il blocco, ovvero creare un nuovo blocco su cui distribuire il carico del blocco pieno, con costo +2.
• Questo richiede una riorganizzazione della struttura per prendere in considerazione il nuovo blocco, questo può richiedere fino a s accessi dove s < 2h+1.
• Infatti nel caso peggiore dobbiamo sdoppiare un blocco per ogni livello.

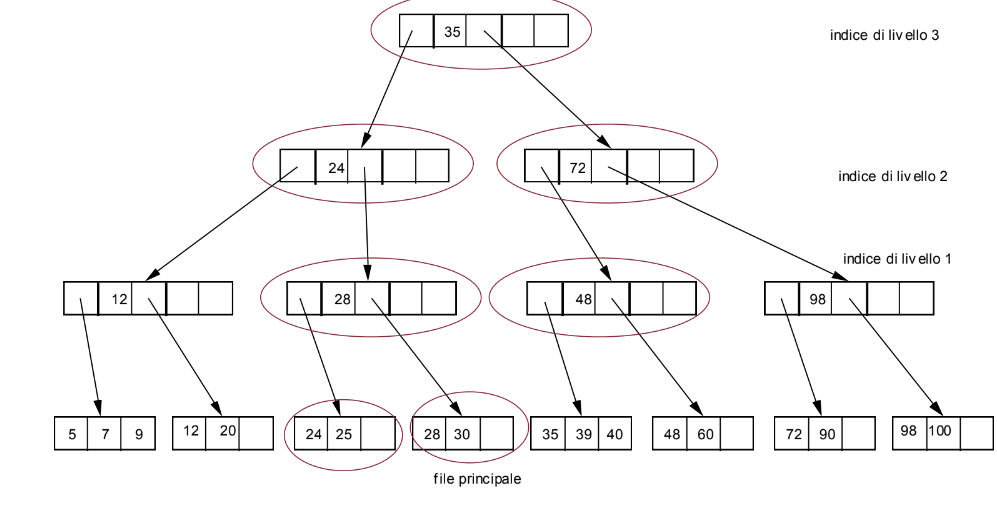
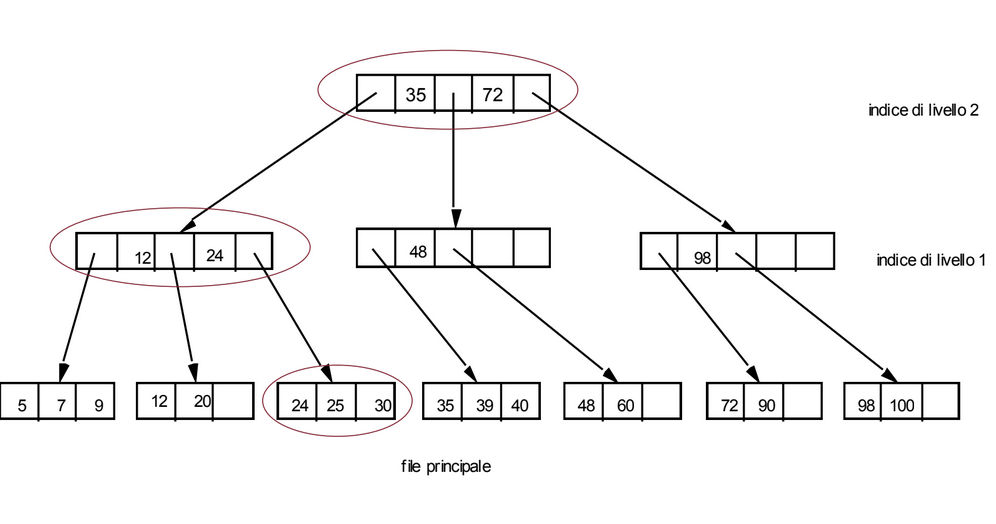
Esempio

Vogliamo inserire il record con chiave 25 ma notiamo che il blocco in cui dovrebbe trovarsi è pieno, dobbiamo quindi riorganizzare la struttura sdoppiando dei blocchi:

---

Cancellazione

Per cancellare un record dobbiamo:

1. Effettuare una ricerca del record (costo h+1)
2. Cancellare il record riscrivendo il blocco senza il record (costo +1)

Il costo cancellazione del record può variare significativamente se dopo la cancellazione, il riempimento del blocco è minore del 50%. In questo caso dobbiamo riorganizzare la struttura, ridistribuendo i record del blocco cancellato.

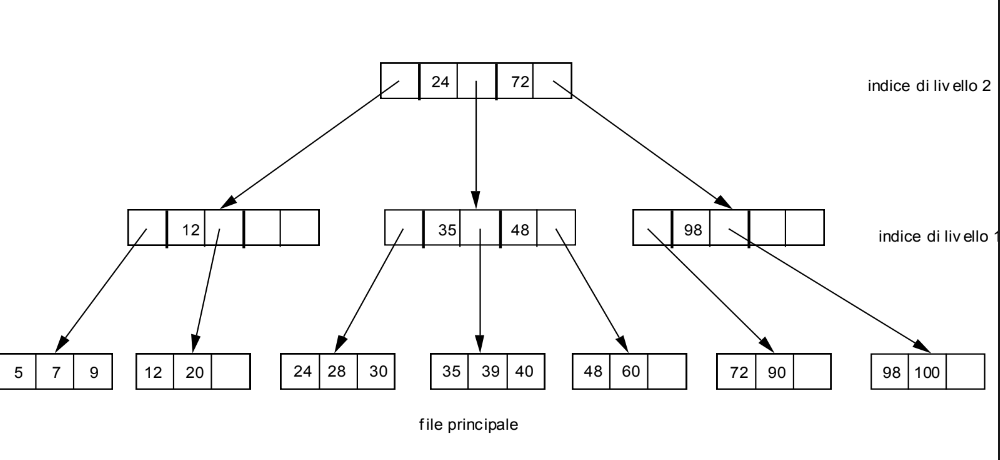
Esempio

Vogliamo cancellare il record con chiave 28 ma se lo facciamo quel blocco rimane con meno della metà dello spazio occupato, quindi riorganizziamo la struttura:

---

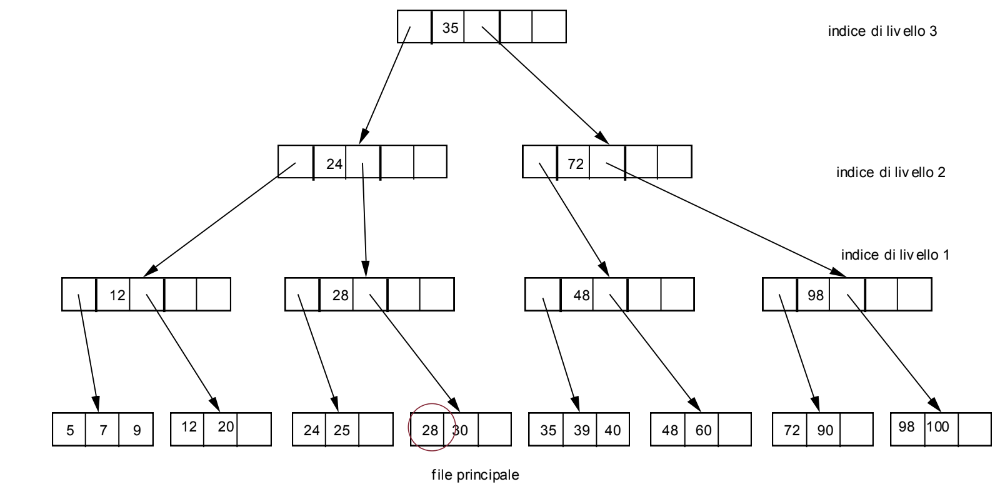
Modifica

Il procedimento di modifica di un record dipende dal fatto che modifica coinvolge o meno campi chiave:

Se la modifica non coinvolge campi chiave, allora:

• Procedimento: dobbiamo effettuare una ricerca del record e poi sovrascriverlo.
• Costo: (h+1) + 1, dove (h+1) costo ricerca e +1 costo accesso di per riscrivere il blocco modificato

Se la modifica coinvolge campi chiave, allora:

• Procedimento: Ricercare il record da modificare, cancellarlo ed inserire un nuovo record con i campi modificati.
• Costo: ricerca + cancellazione + inserimento

Altezza dell’albero

L’altezza dell albero massima la otteniamo quando ogni blocco è riempito al minimo (50%).

lkjnaskjlflfòhjsdlòkfhl da finire