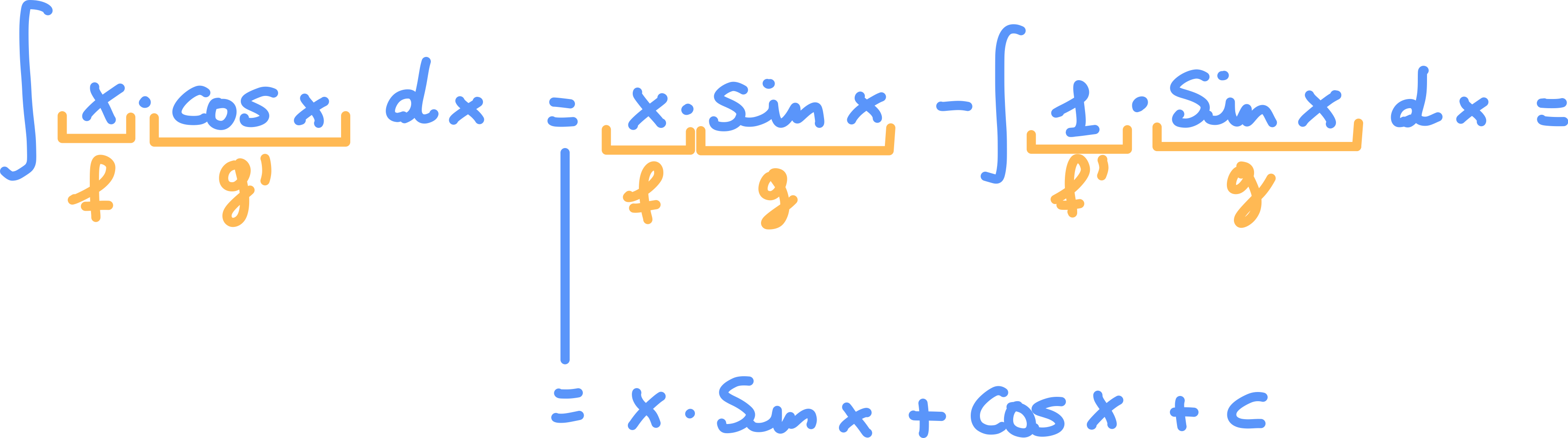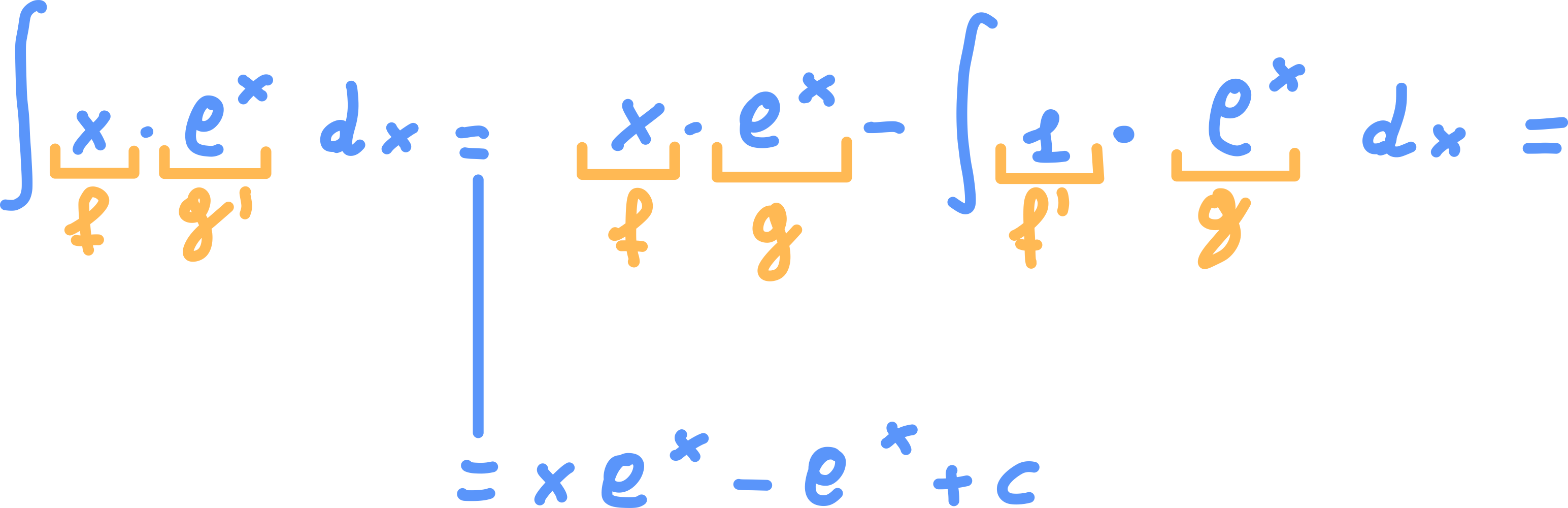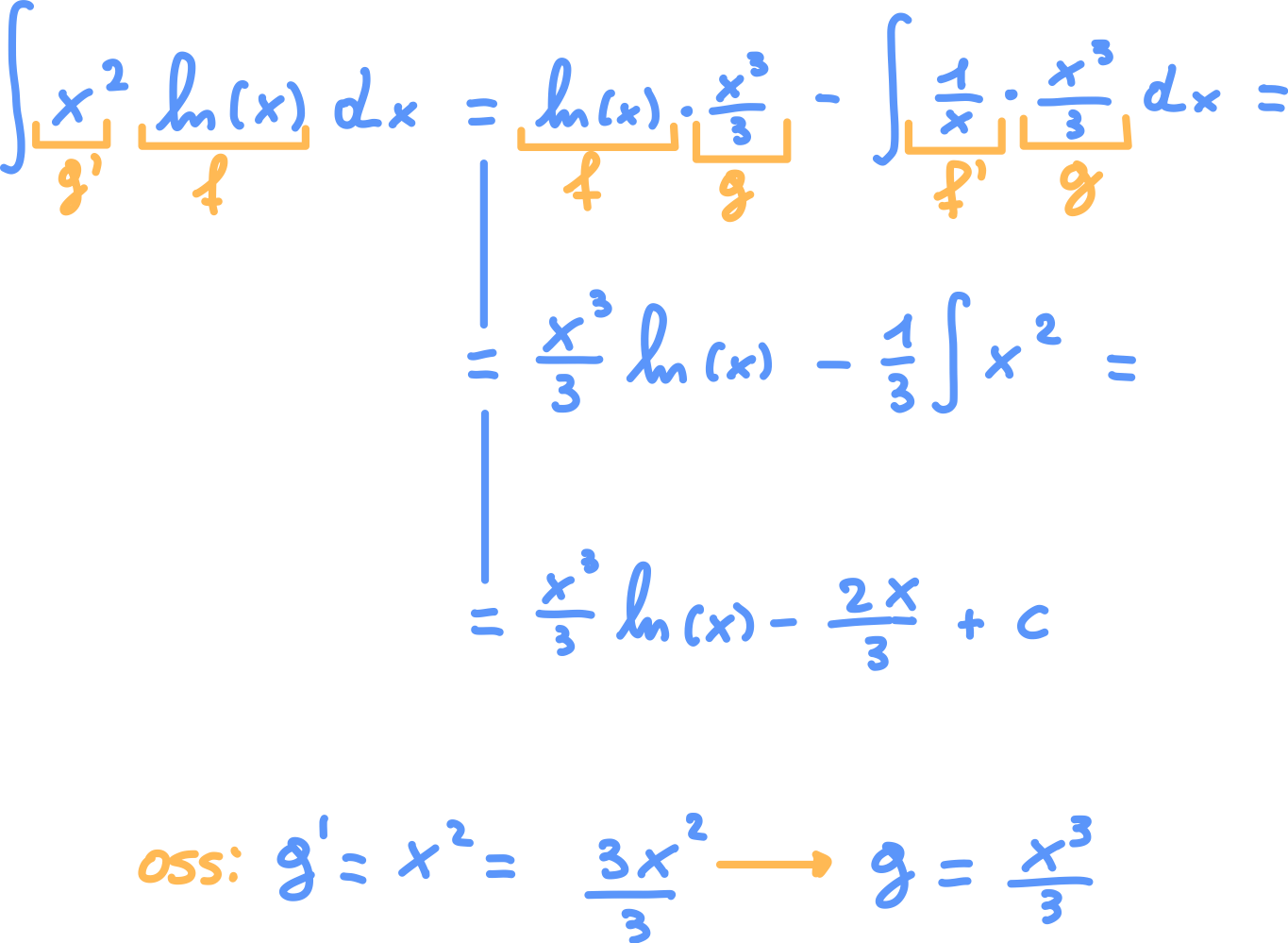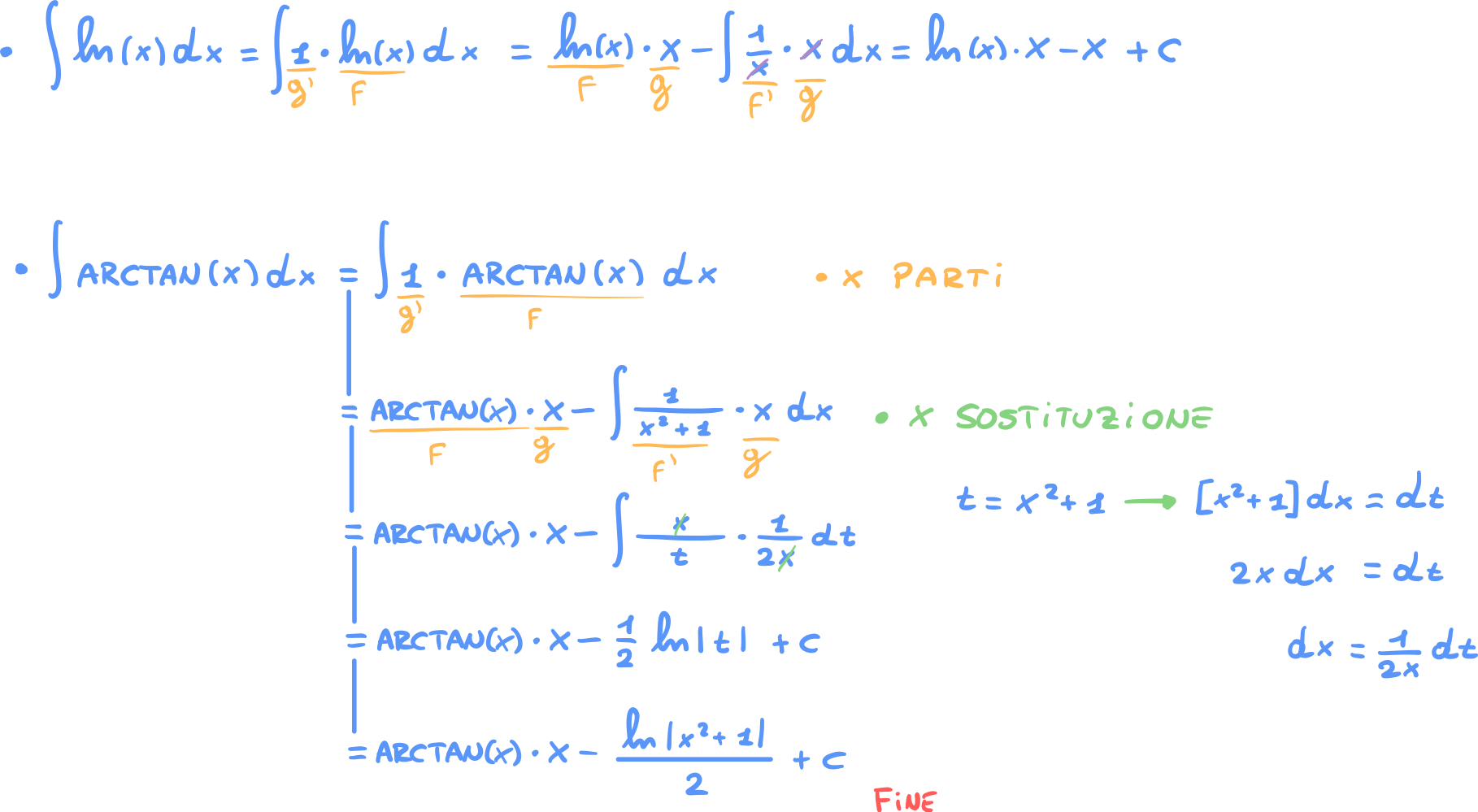Integrazione per Parti

---

Index

1. Introduzione
2. Esempi
3. Integrare per parti due o più volte
4. Integrali Ciclici
5. Fattore differenziale 1

Related

• Integrali
• Calcolo Integrale (class)

---

Introduzione

Metodo utilizzato per semplificare integrali nella forma $\int f(x)g^{\prime }(x)dx$, dove il prodotto tra funzioni $f(x)\cdot g^{\prime }(x)$ è integrabile.

Formula Integrali Definiti

$${\int }_a^{b}f(x)g^{\prime }(x)dx=f(b)g(b)-f(a)g(a)-{\int }_a^b{f}^{\prime }(x)g(x)dx$$

Formula Integrali Definiti

$$\int f(x)g^{\prime }(x)dx=f(x)g(x)-\int f^{\prime }(x)g(x)dx$$

Quando utilizzarlo

L’obbiettivo di questo metodo è quello di trasformare l’integrale originale in un’altra forma più facile da calcolare, ma non è assicurato la nuova forma sia più semplice dell’originale

---

Come usare la formula

Individuare, tra le due funzioni, la derivata $g^{\prime }(x)$ e la primitiva $f(x)$:

• La derivata da individuare, $g(x)$, deve avere una primitiva immediata da calcolare.
• La primitiva $f(x)$ deve avere una derivata $f^{\prime }(x)$ che semplifichi il nuovo integrale $\int f^{\prime }(x)g(x)dx$.

---

Esempi

Esempio 1

Esemepio 2

Esempio 3

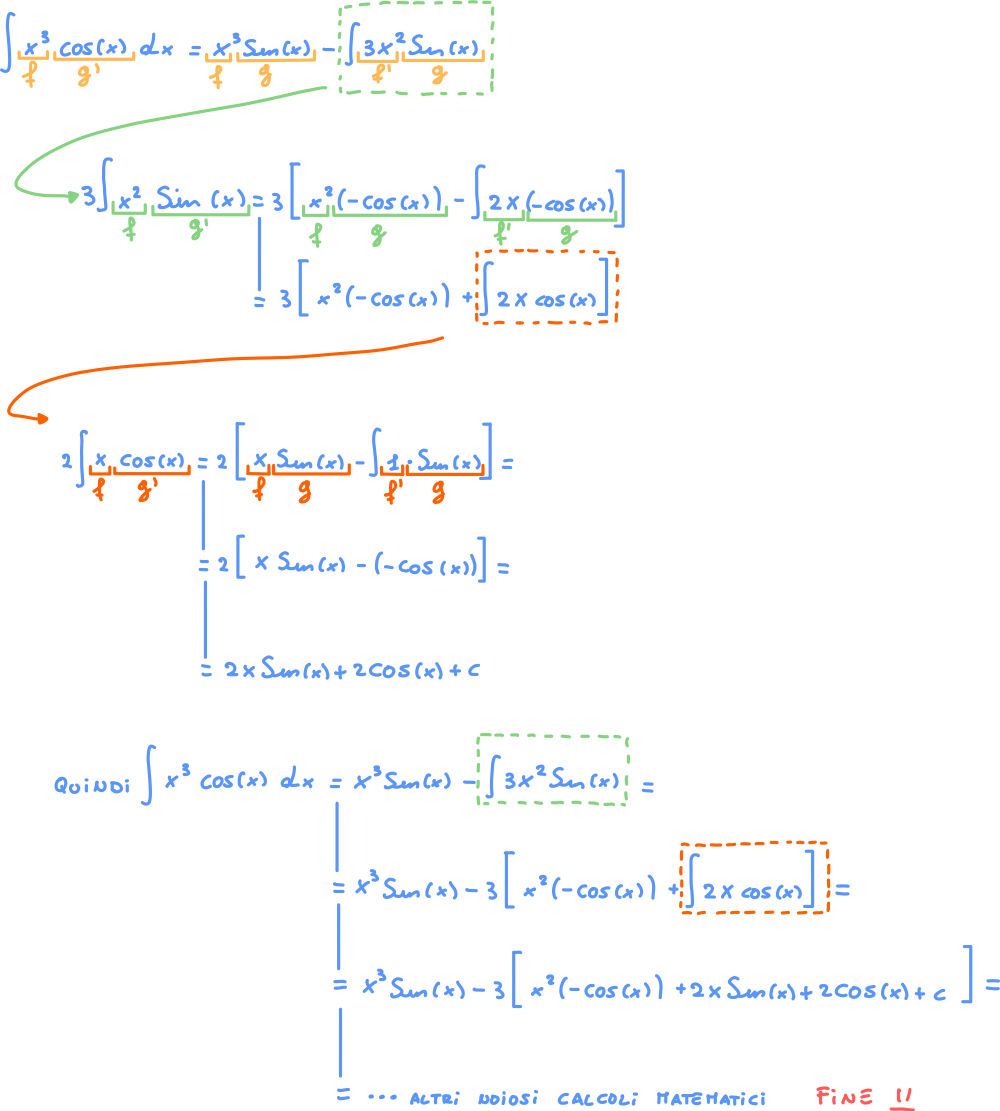
In questo caso serve effettuare l’integrazione per parti più volte vedi Integrare per parti due o più volte per altri esempi

Esempio 4

---

Integrare per parti due o più volte

Quando si hanno integrali di funzioni con derivate cicliche, come ad esempio $\int x^{\alpha }\cdot \sin (x)dx$, $\int x^{\alpha }\cdot \cos (x)dx$ e $\int x^{\alpha }\cdot e^{x}dx$ può capitare di dover riapplicare l’integrazione per parti sul risultato dell’iterazione precedente.

Esempio

---

Integrali Ciclici

Nei casi in l’integrale sia composto dal prodotto di due funzioni con derivate cicliche, non è possibile risolvere l’integrale per part in maniera “classica”, ma basta notare che dopo due integrazioni per parti si riottiene l’integrale originare.

Possiamo sfruttare questa caratteristica per risolvere questa uguaglianza trattandola come una normale equazione.

Esempio

---

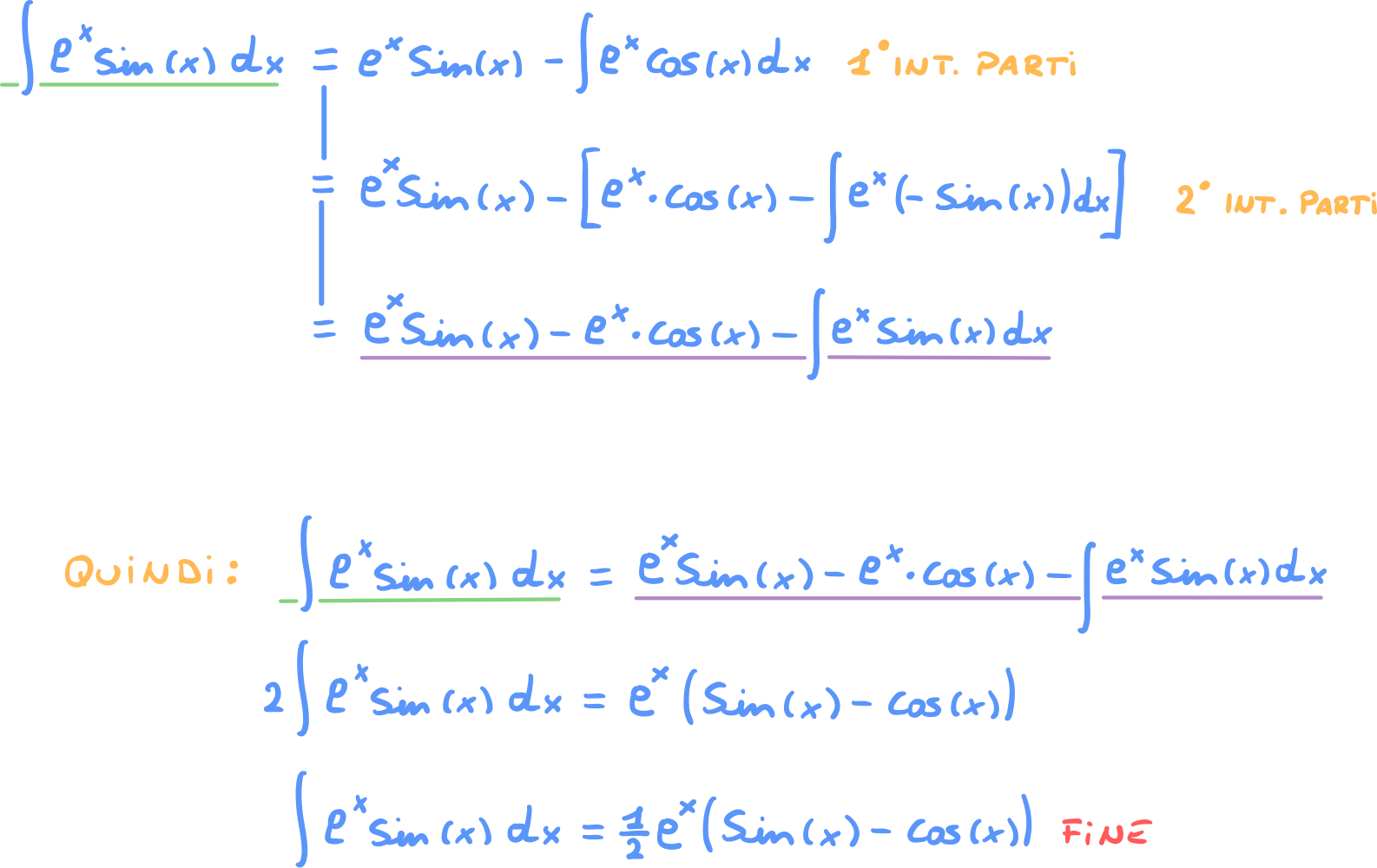
Fattore differenziale 1

Quando si prova ad integrare alcune Funzioni Elementari risulta apparentemente impossibile risolverle con le “classiche” tecniche di integrazione.

Ad esempio con $\int \ln (x)dx$ e $\int \arctan (x)dx$ non risulta possibile utilizzare nessuna tecnica di integrazione, in particolare sembra impossibili utilizzare l’integrazione per parti perché non abbiamo la seconda funzione per il prodotto.

In realtà ci basta considerare $g^{\prime }(x)=1$ e integrare per parti prendendolo come derivata.

Esempio