Funzioni Monotone

Index

1. Monotonia Globale
2. Monotonia Locale

Related

• Funzioni
• Calcolo Differenziale (class)

oss

Calcolo Monotonie con derivate Teorema di Lagrange

---

Monotonia Globale

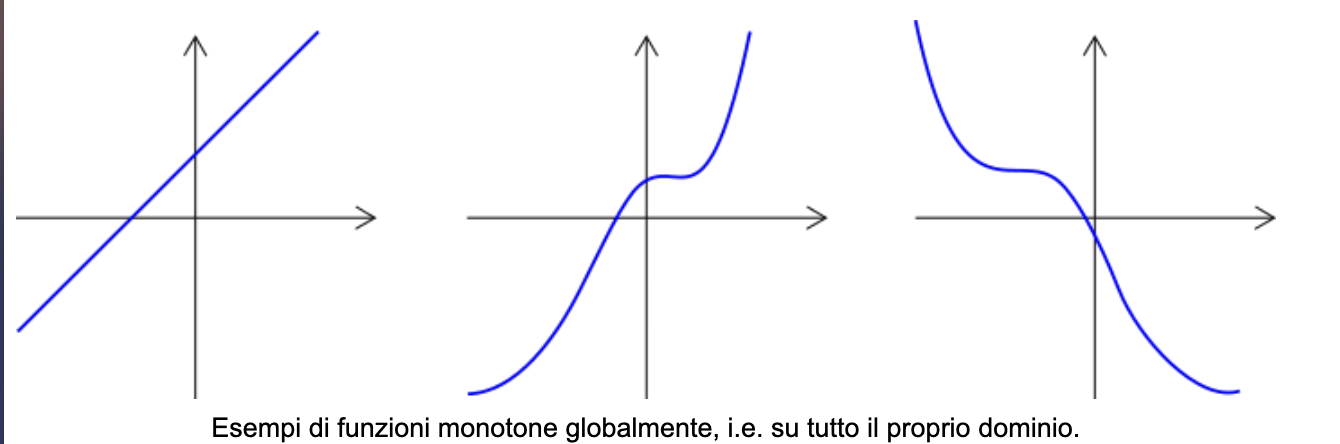
Una funzione si dice monotona se presenta sempre lo stesso andamento

Monotona Crescente

$$\begin{array}{rl}& \forall x_1,x_2\in Dom(f)t.c.x_1\le x_{2}risultache:\\ & \\ & f(x_1)<f(x_2)\end{array}$$

Monotona Non Decrescente = "crescente o stabile":**

\begin{align} &\space\space \forall x_{1},x_{2} \in Dom(f) \space\space t.c.\space\space x_{1}\leq x_{2}\space\space risulta \space\space che: \\ & \\

& ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ f(x_{1}) \leq f(x_{2})\

\end{align}

Monotona Decrescente

$$\begin{array}{rl}& -\forall x_1,x_2\in Dom(f)t.c.x_1\le x_{2}risultache:\\ & \\ & f(x_1)>f(x_2)\end{array}$$

Monotona Non crescente = "decrescente o stabile"

$$\begin{array}{rl}& -\forall x_1,x_2\in Dom(f)t.c.x_1\le x_{2}risultache:\\ & \\ & f(x_1)\ge f(x_2)\end{array}$$

---

Monotonia Locale

Descrive l’andamento di una funzione in un determinato intervallo del dominio

Monotonia Locale Crescente

\begin{align} & \space\space Dato ~~ I\in Dom(f)~~ e ~~ x_{1},x_{2}\in I ~~ t.c. ~~ x_{1} \leq x_{2}~~risulta \space\space che: \\ & \\ & ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ f(x_{1}) \leq f(x_{2})\\ \end{align} $$

Monotonia Locale Decrescente

\begin{align} & \space\space Dato ~~ I\in Dom(f)~~ e ~~ x_{1},x_{2}\in I ~~ t.c. ~~ x_{1} \leq x_{2}~~risulta \space\space che: \\ & \\ & ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ f(x_{1}) \geq f(x_{2})\\ \end{align} $$