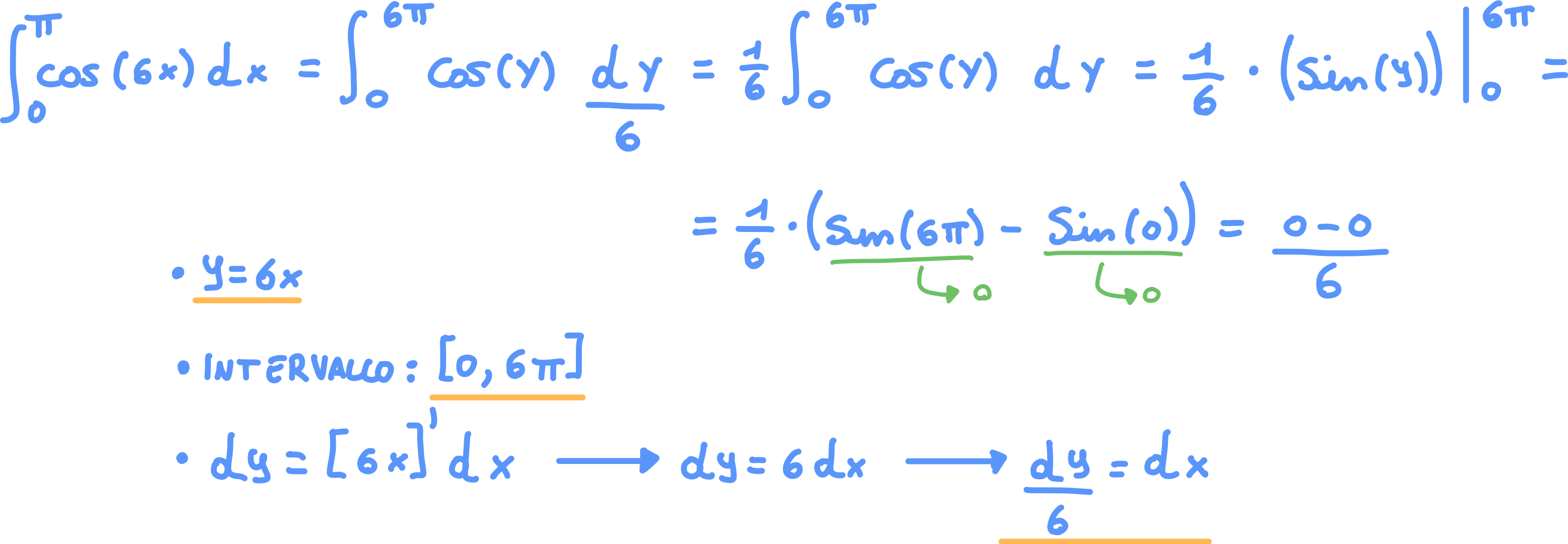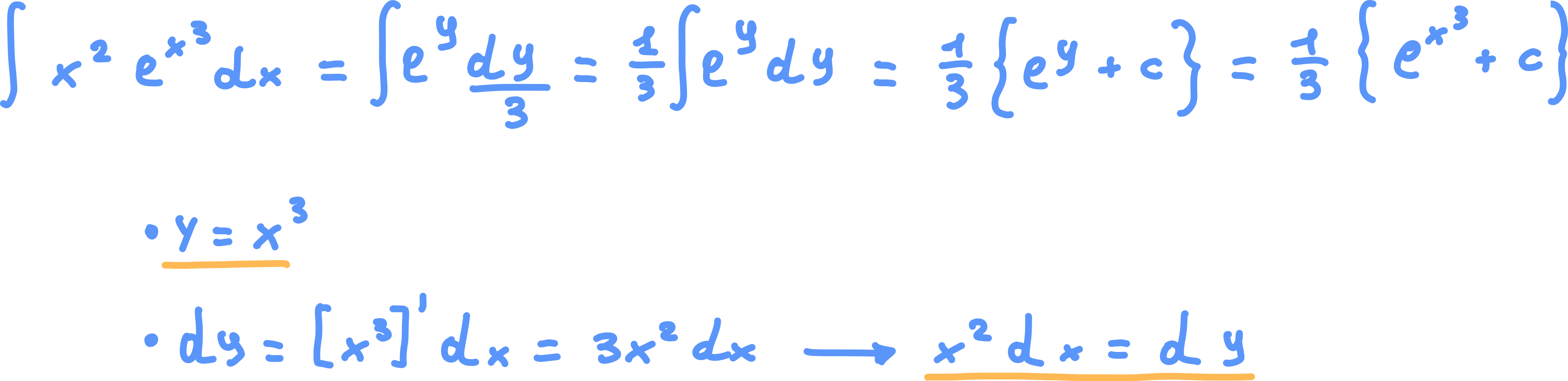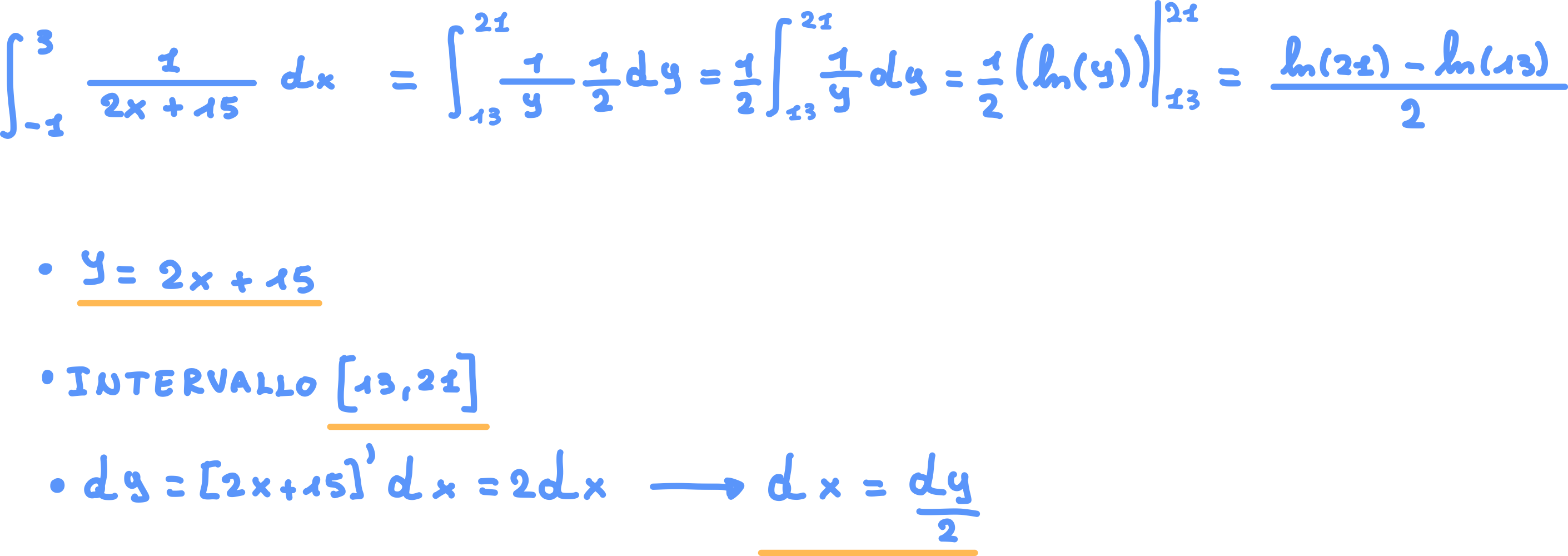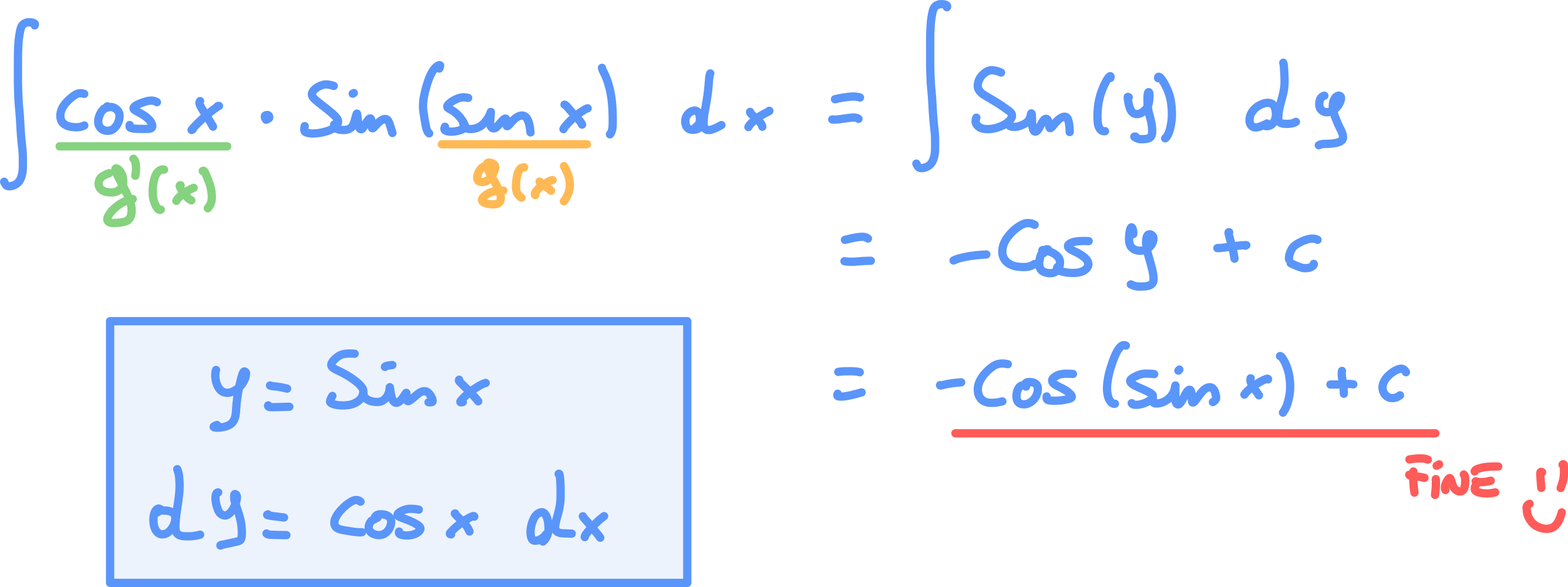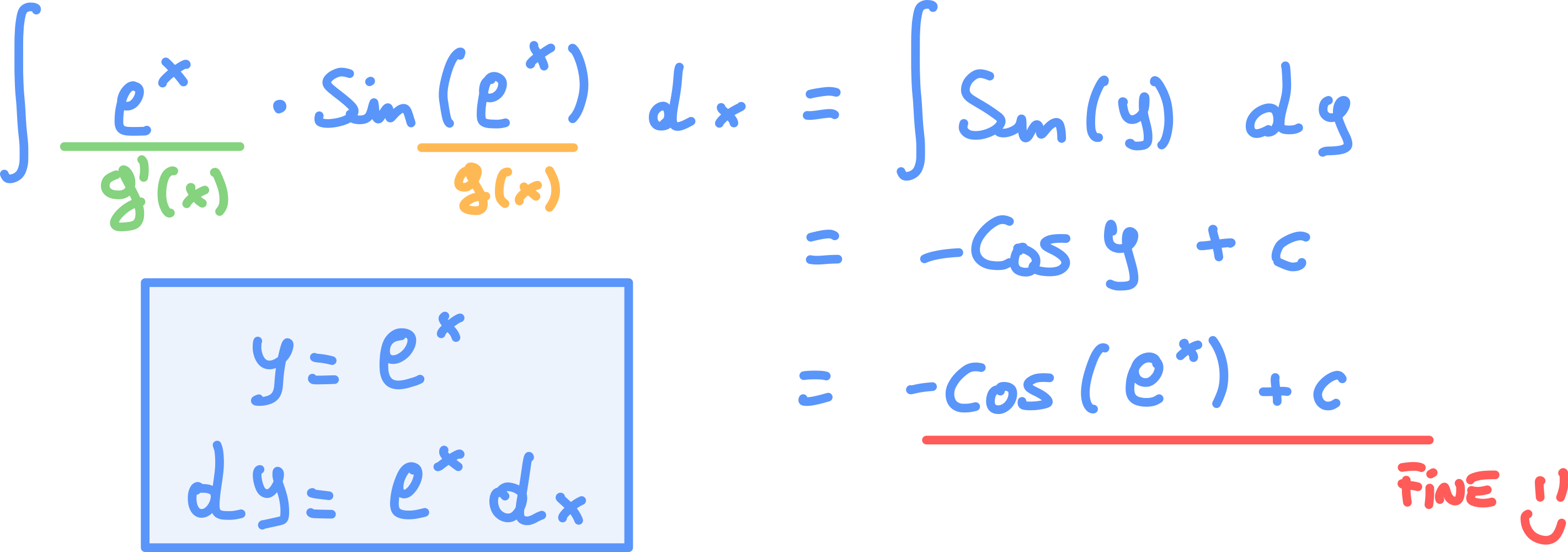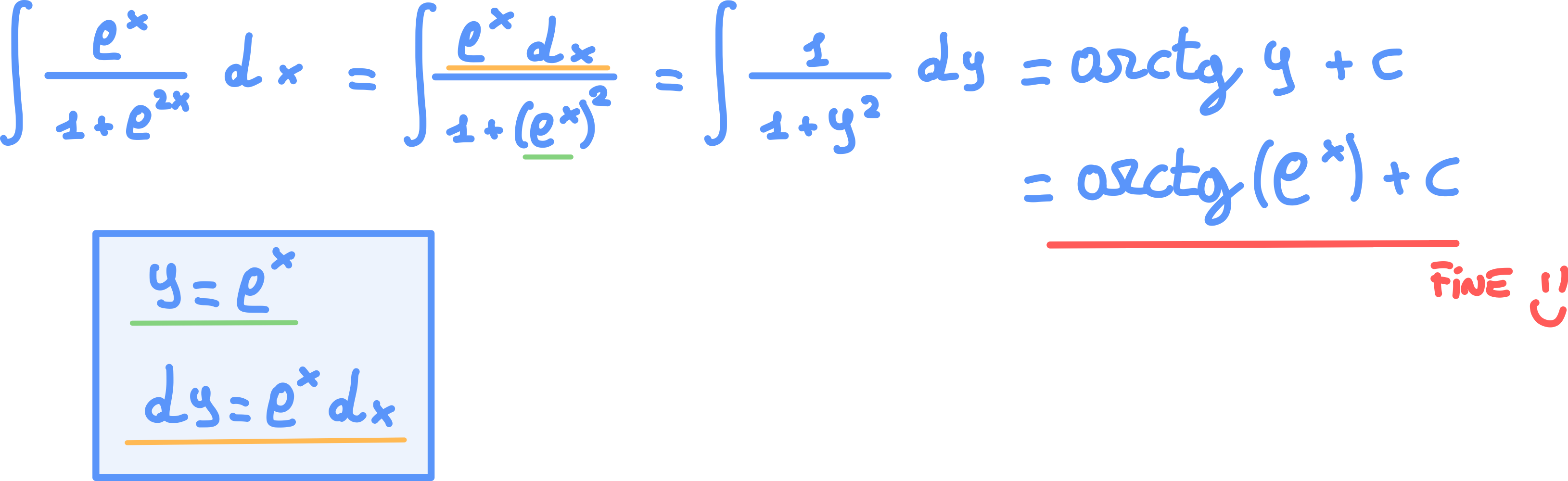Integrazione per Sostituzione

---

Index

1. Integrazione per Sostituzione
2. Sostituzione per gli Integrali Composti

Related

• Integrali
• Calcolo Integrale (class)

---

Integrazione per Sostituzione

Introduzione

Alcuni integrali possono essere ricondotti ad integrali noti/integrali di funzioni elementari di cui è facile trovare la primitiva.

In questi casi possiamo utilizzare il metodo dell’integrazione per sostituzione per risolverli, effettuando un cambio di variabile andando a sostituire ogni riferimento alla variabile originale presente nell’integrale, inclusi gli estremi dell’intervallo e la variabile di integrazione.

Metodo

L’integrale

$${\int }_1^4{e}^{3x}$$

è molto simile all’integrale di $f(x)=e^x$ il cui risultato sappiamo essere $F(x)=e^x$, applichiamo il metodo della sostituzione:

• Poniamo $y=3x$ al fine di trasformare $f(x)=e^{3x}=e^y$
• Gli estremi dell’intervallo devono essere modificati poiché quando $x=1$ abbiamo che $y=3\cdot 1=3$, mentre quando $x=4$ abbiamo che $y=3\cdot 4=12$
• Anche la variabile di integrazione deve essere modificata, poiché se $y=3x$, ne segue che $y^{\prime }=[3x{]}^{\prime }=3$

$$\begin{array}{rl}& y=3x\\ & dy=[3x{]}^{{}^{\prime }}dx\\ & dy=3dx\\ & \frac{dy}{3}=dx\end{array}$$

Dunque, una volta sostituiti tutti i riferimenti alla variabile di integrazione, l’integrale che otterremo sarà:

$${\int }_1^4{e}^{3x}dx={\int }_3^{12}{e}^y\frac{dy}{3}=\frac{1}{3}{\int }_3^{12}{e}^{y}dy$$

A questo punto, ci basterà calcolare l’integrale immediato ottenuto, per poi riportare il risultato ottenuto in termini della variabile di integrazione originale:

$$\frac{1}{3}{\int }_3^{12}{e}^{y}dy=\frac{e^y}{3}{|}_3^{12}=\frac{e^{3x}}{3}{|}_1^4=\frac{e^{12}-e^3}{3}$$

Esempio 1

Esempio 2

Esempio 3

---

Sostituzione per gli Integrali Composti

Introduzione

Tecnica per la Risoluzione di integrali composti basata sulla formula:

$${\int }_a^{b}f(g(x))\cdot g^{\prime }(x)dx={\int }_{g(a)}^{g(b)}f(y)dy$$

Vedi: Integrali di Funzioni Composte

Metodo

${\int }_a^{b}f(g(x))\cdot g^{\prime }(x)dx$

1. Calcolare nuova variabile di integrazione:

• $y=g(x)$
• $dy=g^{\prime }(x)dx$

2. Calcolare nuovi estremi di integrazione:

• $a\to g(a)$
• $b\to g(b)$

3. Risolvere integrale per y:

• ${\int }_{g(a)}^{g(b)}f(y)dy$
• Sostituire la $y$ del risultato dell’integrale con $g(x)$
• Risolvere

Esempio 1

Esempio 2

Esempio 3

---