Numeri binari con virgola mobile (floating point)

Index

1. Introduzione
2. Standard IEEE754
3. Notazione scientifica
4. Conversioni
5. Bias
6. Operazioni

Related

• Sistema di numerazione binario
• Sistemi numerici
• Progettazione Sistemi Digitali (class)

---

Introduzione

Ogni numero binario in virgola mobile è composto da una tripla di valori:

1. Segno (pos 0, neg 1)
2. Esponente (quanti numeri fanno parte della parte intera)
3. Mantissa (cifre dopo la virgola)

Vantaggi

• Rappresentazione mobile permette di ottimizzare al massimo l’utilizzo dei bit a disposizione, permettendo di utilizzare il miglior rapporto tra precisione della parte intera e della parte decimale in base al numero che dobbiamo rappresentare

Svantaggi

• Conversione meno intuitiva per l’essere umano

---

Standard IEEE754

Lo standard IEEE754 ha 3 categorie che variano nella precisione della rappresentazione

Half precision

• Totale: 16 bit
• Segno: 1 bit
• Esponente: 5
• Mantissa: 10

Single Precision

• Totale: 32 bit
• Segno: 1 bit
• Esponente: 8 bit
• Mantissa: 23 bit

Double Precision

• Totale: 64 bit
• Segno: 1 bit
• Esponente: 11 bit
• Mantissa: 52 bit

---

Notazione scientifica

Capire la notazione scientifica di un numero in binario è fondamentale per capire il funzionamento della virgola mobile

Lo stesso principio che si utilizza per la notazione scientifica di un numero in base 10 si può utilizzare per un numero in binario ma utilizzando potenze di due

---

Conversioni

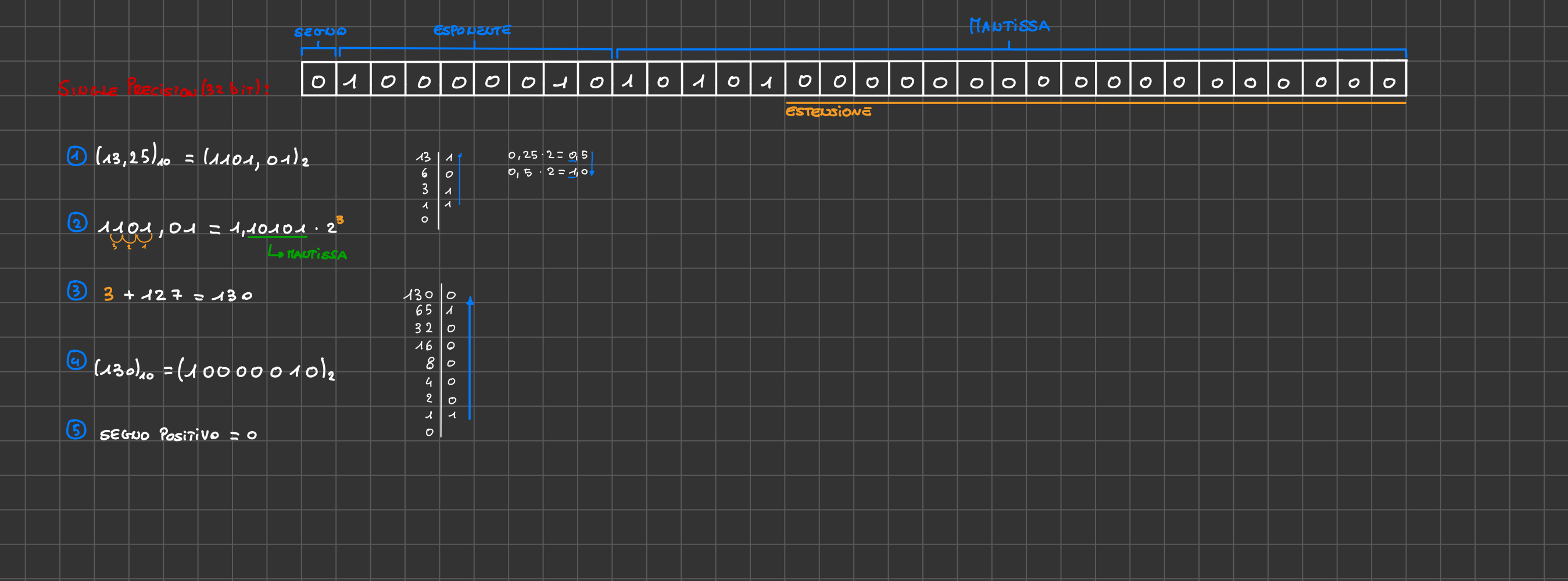
B10 → B2 Floating Point

1. Converto il numero in binario (utilizzando metodo virgola fissa)
2. Sposto la virgola, trovando mantissa e l’esponente (forma: 1,M * 2^e )
3. Aggiungo bias all’esponente (k)
4. Converto esponente in binario
5. Scrivo segno (pos = 0, neg = 1)

B2 Floating Point → B10

1. Utilizzare formula:

$$(-1{)}^s\cdot (1,M)\cdot 2^{e-k}$$

1. Convertire risultato in decimale usando metodo fixed point b2→b10

oss:

• s = segno
• M = mantissa
• e = esponente
• k = bias

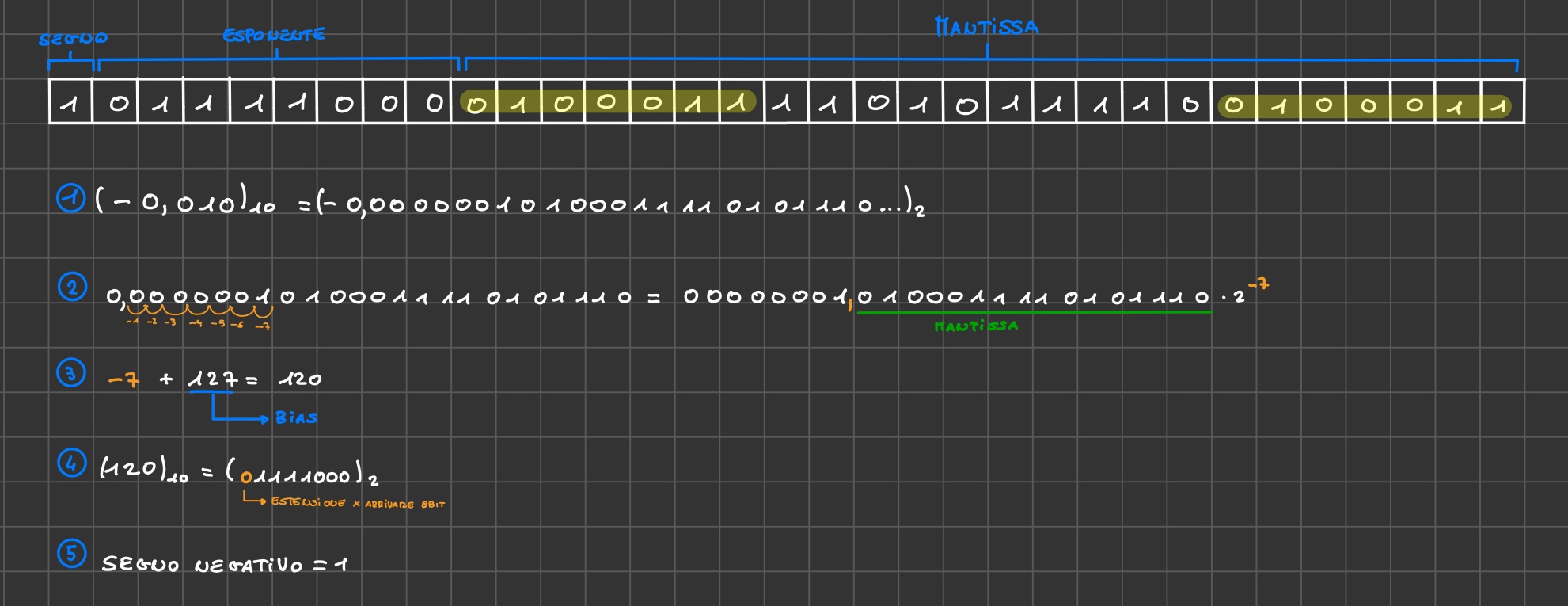
Conversione numeri periodici

Quando si ha un numero binario periodico (virgola fissa) per rappresentarlo in virgola mobile bisogna avere degli accorgimenti

Quando si scrive la mantissa e non si anno abbastanza cifre per completarla invece di estenderla con degli zeri va estesa ricopiando la parte iniziale della mantissa

---

Bias

Il bias è un valore che dipende dalla precisione di rappresentazione, il suo scopo è correggere l’errore di bias negli esponenti.

Valori del bias

• Half precision: ?
• Single Precision: 127
• Double Precision: ?

Come si calcola?

$$2^{E-1}-1$$

oss: E è il numero di bit dell’esponente

---

Operazioni

Addizione

1. Normalizziamo i due numeri (ovvero stesso esponente)
2. Mantissa più grande sopra, più piccola sotto
3. Se segno concorde somma se discorde sottrazione
4. Segno del risultato è segno del più grande

Sottrazione

1. Normalizziamo i due numeri (ovvero stesso esponente)
2. Mantissa più grande sopra, più piccola sotto
3. Se segno concorde somma se discorde sottrazione
4. Segno del risultato è segno del più grande

Prodotto

1. Sommare (prodotto) / sottrarre (differenza) gli esponenti
2. Mantissa più grande va sopra, più piccola sotto
3. Moltiplicare / dividere le mantisse
4. Segno:

• Negativo (operandi discordi)
• Positivo (operandi concordi)

5. l risultato potrebbe essere normalizzato (ovvero riportare alla rappresentazione standard (1,M) aggiustando esponente)

Divisione

1. Sommare (prodotto) / sottrarre (differenza) gli esponenti
2. Mantissa più grande va sopra, più piccola sotto
3. Moltiplicare / dividere le mantisse
4. Segno:

• Negativo (operandi discordi)
• Positivo (operandi concordi)

5. l risultato potrebbe essere normalizzato (ovvero riportare alla rappresentazione standard (1,M) aggiustando esponente)