iconNotes in Public

Sistema di numerazione binario

Jan 18, 20253 min read

Index

  1. Introduzione
  2. Conversioni
  3. Rappresentazione binaria dei numeri decimali
  4. Operazioni
  5. Over-flow e Under-flow
  6. Rappresentazione numeri negativi in binario
  7. Rappresentazione numeri reali in binario

Related

Introduzione

Conversioni

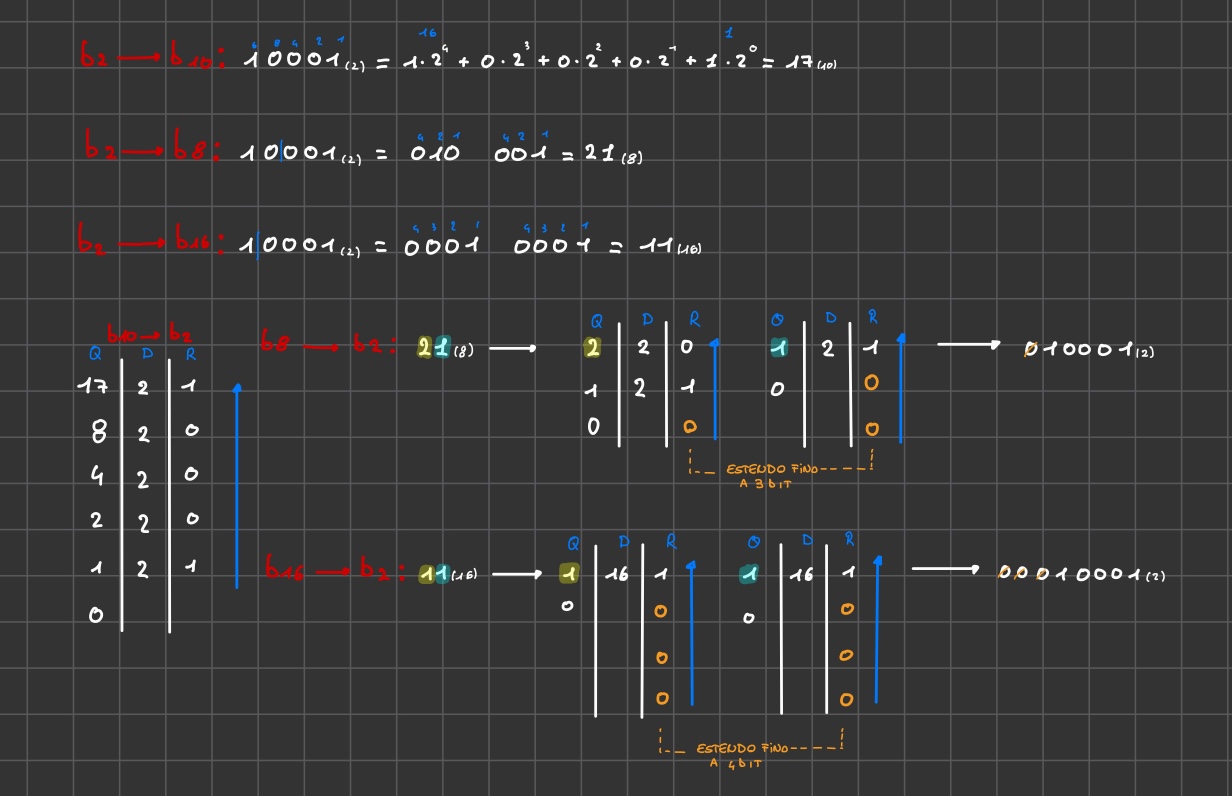
Conversione base2 ⇒ base b

  1. Partendo dalla prima cifra a destra assegniamo la posizione alla cifre che compongono il numero partenza

  2. Moltiplichiamo la prima cifra (pos b0) per la potenza 2^0, la seconda per 2^1, la terza per 2^2, e cosi via fino ad esaurire tutte le cifre

  3. Sommando i valori trovati al punto 2 avremo il numero espresso nel sistema di numerazione decimale

oss: se in base 8 o 16 bisogna suddividere il numero binario in sottogruppi di 3 cifre (se b2→b8) o 4 cifre (se b2→b16) e trattarle come se fossero delle conversioni a se, soltanto alla fine si devono unire i risultati per ottenere la cifra finale

Conversione Base b ⇒ base2

  1. Dividere il numero N (base b) per la base 2, ottenendo così un quoziente e un resto

  2. Dividere il quoziente dell’ultima operazione per 2, ricavando un nuovo quoziente e un nuovo resto

  3. Continuare a dividere i quozienti ottenuti per i fino a quando non si ottiene un quoziente uguale a zero

  4. I resti della divisione, scritti in ordine inverso rispetto a come li abbiamo ottenuti, formano le cifre del numero N espresso in base 2

oss se N è in base 8 o 16:

  • si dive dividere N nelle sue sotto cifre ed effettuare questo procedimento per ognuna delle cifre
  • ci potrebbe essere il bisogno di estendere i risultati

Esempi

Esempio: Conversioni_sistemi_numerici.pdf

Rappresentazione binaria dei numeri decimali

Calcolare bit necessari per rappresentare numero di N cifre

Calcolare numero di cifre rappresentabili da N bit

Conversioni potenze binario → decimale

  • Kilo = 2^10 = 1024 ~ 10^3 = 1000
  • Meg = 2^20 = … = 10^6 = 1 milione
  • Giga = 2^30 = … = 10^9 = 1 miliardo

Operazioni

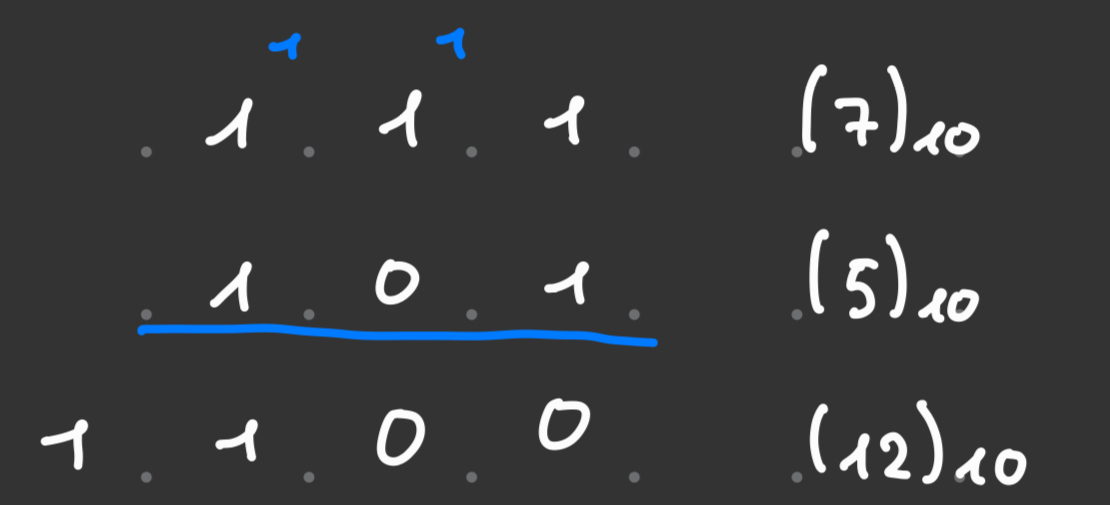
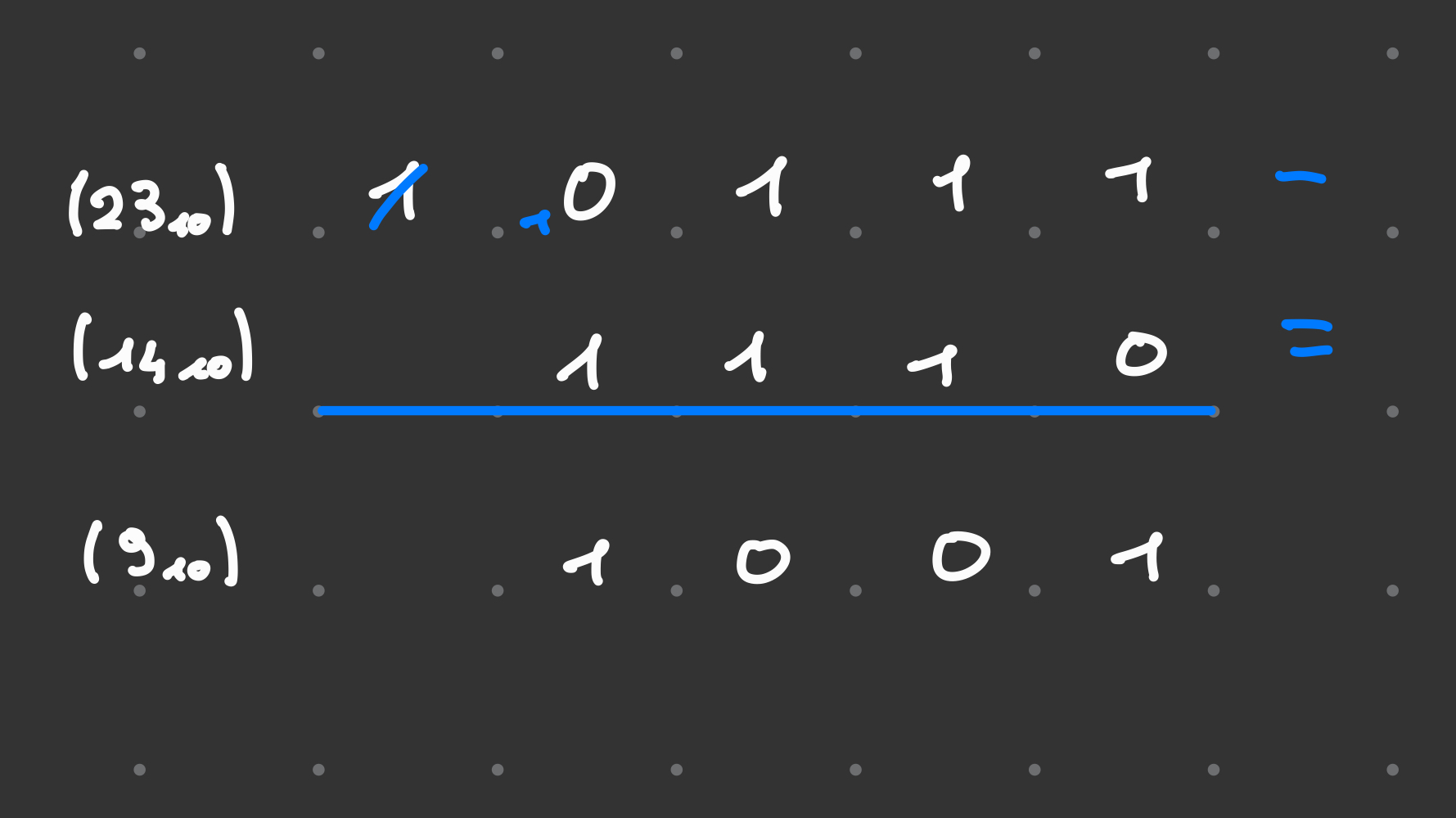
La somma e la sottrazione tra numeri binari avviane allo stesso modo della summa tra numeri in base 10

Somma

Sottrazione

Prodotto

oss: Quando si effettua una moltiplicazione il risultato deve essere rappresentato sempre con il doppio dei bit rispetto agli operandi

Over-flow e Under-flow

Quando si effettuano operazioni su macchine digitali c’è il rischio di sforare i limiti di architettura/memoria dedicata per la ripresentazione numerica

Questi avvenimenti vengono chiamati:

Rappresentazione numeri negativi in binario

Esistono diversi modi per rappresentare numeri negativi in binario:

Nota

Tutti e tre i metodi sono accomunati dal fatto che il bit più significativo indica la negatività (se 1) o la positività (se 0) della rappresentazione

Metodi per conversioni:

  • Converti B10 → B2
  • Aggiungi bit segno (most significant bit) inizialmente a 0

MS:

  • Se Negativo: Bit segno = 1
  • Se Positivo: non fare niente

CA1:

  • Se Negativo: inverti 1 e 0 e vice versa
  • Se Positivo: non fare niente

CA2:

  • Se Negativo:
    1. inverti 1 e 0 e vice versa
    2. somma 1 al least significant bit
  • Se Positivo:
    1. non fare niente

Rappresentazione numeri reali in binario

In binario esistono due modi per rappresentare i numeri reali:

  1. Numeri binari con virgola fissa (fixed point) 🟡 (aggiungere operazioni)
  2. Numeri binari con virgola mobile (floating point) 🟢

Graph View

Backlinks