Index
- Definizione
- Bit di segno
- Intervalli di rappresentazione
- Conversione (metodo circuitale)
- Conversione (metodo semplificato)
- Somma complemento a due
- Sottrazione complemento a due
- Casi Particolari con Somma/Sottrazione
- Estensione rappresentazione utilizzando complemento a due
- Over-flow e Under-flow con complemento a due
- Over-flow
- Under-flow
Related
Introduzione
Il complemento a due, o complemento alla base, è il metodo più diffuso per la rappresentazione dei numeri con segno in informatica.
La sua enorme diffusione è data dal fatto che i circuiti di addizione e sottrazione non devono esaminare il segno di un numero rappresentato con questo sistema per determinare quale delle due operazioni sia necessaria, permettendo tecnologie più semplici e con maggiore precisione; si utilizza un solo circuito, il Circuiti Aritmetici, sia per l’addizione che per la sottrazione.
Esempio
Vantaggi
- Non richiede il controllo del bit di segno per effettuare le operazioni
- Esecuzione di operazioni di somma e sottrazione con lo stesso circuito
- Calcolo dell’opposto relativamente semplice, leggi:
Bit di segno
Il bit di segno è il bit più a sinistra (bit più significativo) della sequenza binaria di un numero a complemento a 2, questo se è:
- 0 allora il numero è positivo
- 1 allora il numero è negativo
oss: La rappresentazione minima in complemento a 2 richiede sempre l’utilizzo di un bit in più rispetto alla rappresentazione in binario puro
Esempio
Intervalli di rappresentazione
Con n bit si possono rappresentare numeri nell’intervallo:
Quindi si possono rappresentare 2^n numeri, di cui:
Osservazioni
- è possibile rappresentare un numero in meno positivo rispetto ai negativi perché in realtà la codifica del numero 0 fa parte dei numeri positivi.
- Si dice Rappresentazione asimmetrica.
Conversione (metodo circuitale)
Metodo
- Scrivere numero in binario (aggiungendo 0 come bit di segno se non è già esteso)
- invertire gli 1 con gli 0 e vice versa
- Sommare 1
Esempio
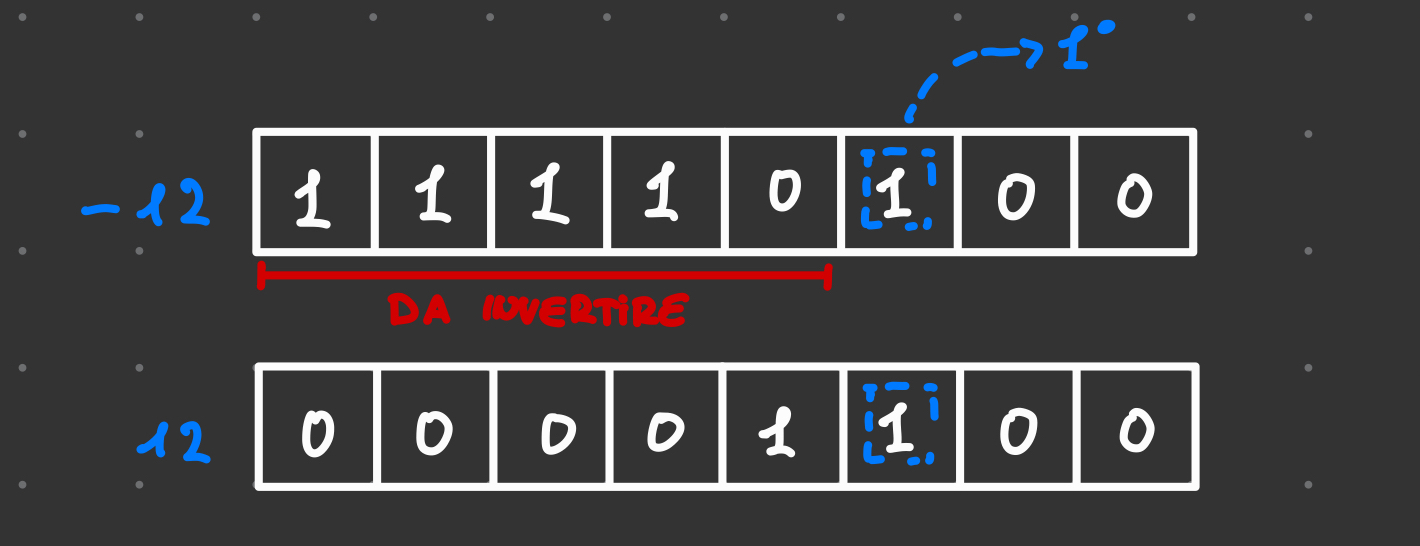
Conversione (metodo semplificato)
Metodo
- Trovare il primo 1 della sequenza binaria (da sinistra verso destra)
- Invertire tutti i valori dopo quell’1
Esempio
Somma complemento a due
Metodo
Convertiamo i numeri in binario non tenendo conto del segno
Utilizziamo il complemento a due per per convertire i numeri negativi
Effettuo operazione di somma con il metodo standard per i numeri in base 2
Effettuiamo la conversione del risultato da complemento a due a decimale
oss: se il most significant bit è 1 il numero in base 10 e negativo
Esempio
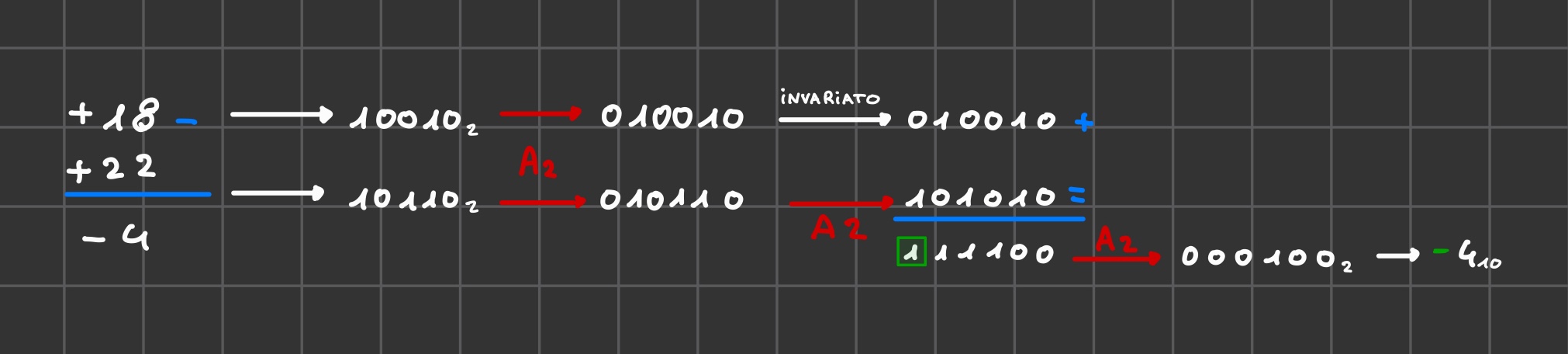
Sottrazione complemento a due
Metodo
- Convertiamo i numeri in binario non tenendo conto del segno
- Utilizziamo il complemento a due per per convertire i numeri negativi
- Inverto il segno di n2:
- Effettuo operazione di somma
- Effettuiamo la conversione del risultato da complemento a due a decimale
Esempio
Casi Particolari con Somma/Sottrazione
Somma tra numeri di cui almeno uno dei due non è negativo
Quando avviene un over-flow in questo caso, non deve essere preso in considerazione
Over-flow somme tra due numeri negativi
Quando si effettua una somma tra numeri negativi è certo che avvenga un over-flow, possono avvenire due situazioni distinte:
1. Escludendo l’overflow il bit di segno del risultato è sbagliato (0):
- Soluzione: Utilizzare bit di over-flow come bit di segno
2. Escludendo l’overflow il bit di segno del risultato è giusto (1)
- in questo caso, indipendentemente dal fatto che utilizzeremo o no il bit di overflow come bit di segno il risultato sarà giusto!
Mancanza di bit per la rappresentazione
Sommando c’è il rischio di non avere abbastanza bit per rappresentare il risultato
- Soluzione estendere gli operandi e ripetere l’operazione
Estensione rappresentazione utilizzando complemento a due
Estensione di numero positivo
Se numero inizia con 0 aggiungo tanti zeri quanto voglio estendere
Estensione di numero negativo
Se numero inizia con 1 aggiungo tanti uni quanto voglio estendere
Esempi:
Over-flow e Under-flow con complemento a due
Con Over-flow e Under-flow si indica il superare il numero di bit necessari per rappresentare un determinato numero rispetto al numero di bit di cui si a disposizione (limitazione che può essere imposta dall’architettura o dal software), avviene quando si operazioni sui numeri
Over-flow
In particolare quando questo avviene in un sistema che utilizza il complemento a due è possibile accorgersene da fatto che il bit del segno assume valori impossibili. (esempio la somma di due numeri negativi da un risultato positivo)
oss: basta controllare bit di segno per verificare l’avvenimento di un over-flow
Per calcolare il numero risultante dobbiamo calcolare di quanto stiamo “sforando” es. se vogliamo rappresentare il numero 9 ma la nostra architettura (4bit) permette di rappresentare massimo il 7 stiamo “sforando” di 2, quando si sfora in realtà si sta saltando dal lato opposto del range e si avanza di quanto si a sforato
Esempio
Under-flow
In particolare si parla di Under-flow quando proviamo a rappresentare un numero Negativo più piccolo rispetto al numero negativo minimo rappresentabile dal numero di bit a disposizione.
Per risolvere dobbiamo fare aumentare il numero di bit a nostra disposizione per la rappresentazione utilizzando in metodo dell’ estensione
Estensione
Per estendere un numero basta aggiungere un nuovo bit più significativo (tutto a sinistra), in particolare in CA2 se dobbiamo estendere un numero:
- Positivo: aggiungiamo uno 0
- Negativo: aggiungiamo un 1
Esempio