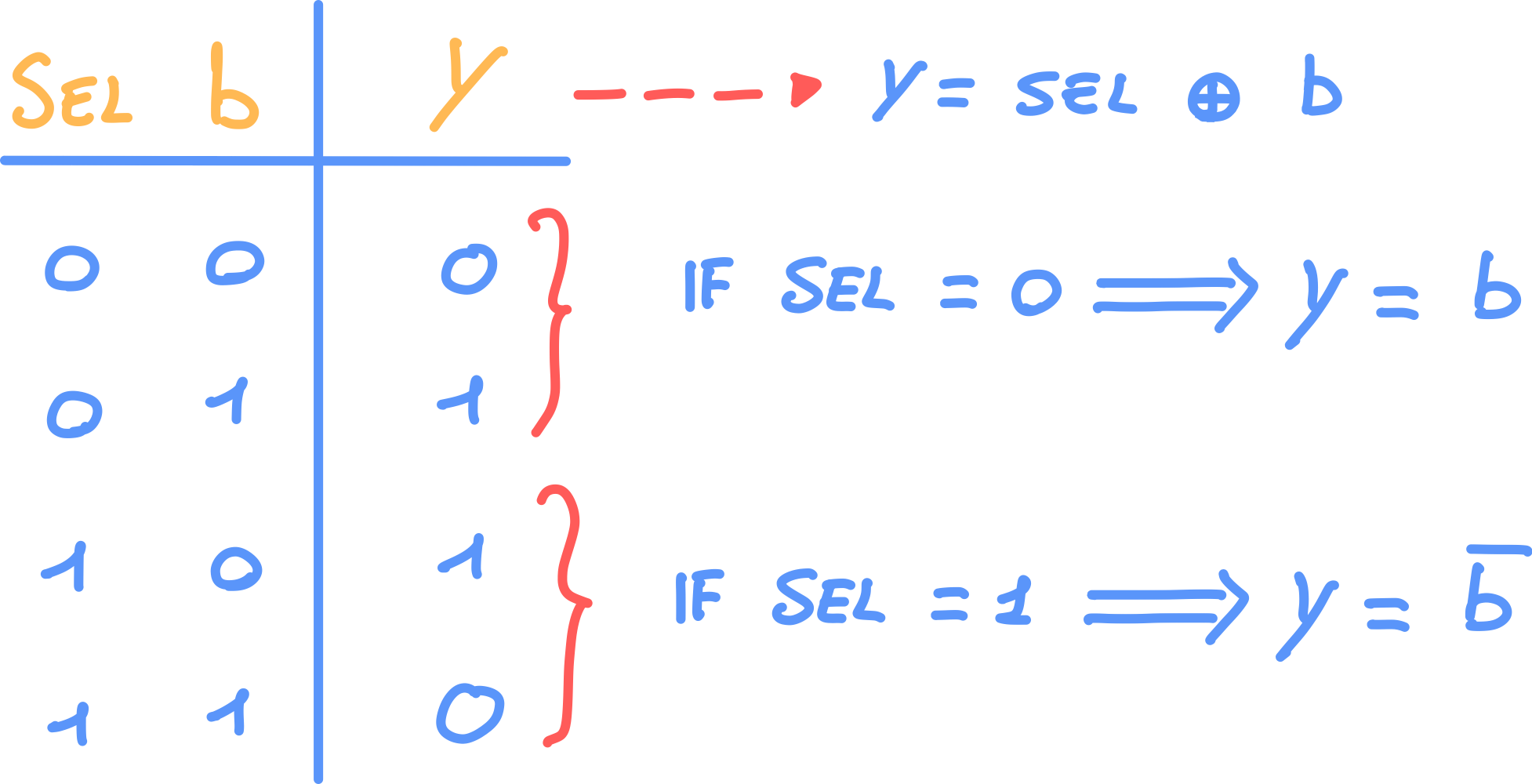Index
Related
- Ripple Carry Adder
- Circuiti Aritmetici
- Circuiti combinatori
- Digitali (class)]]
Introduzione
Come vedremo il Ripple Carry Adder per effettuare la sottrazione utilizzerà l’codifica CA2,
Quindi la sottrazione di due numeri non è altro che la somma del primo con il complemento ca2 del secondo.
Complemento CA2?
Per complementare un numero in CA2 serve:
- Negare tutti i singoli bit che compongono il numero
- Sommare 1
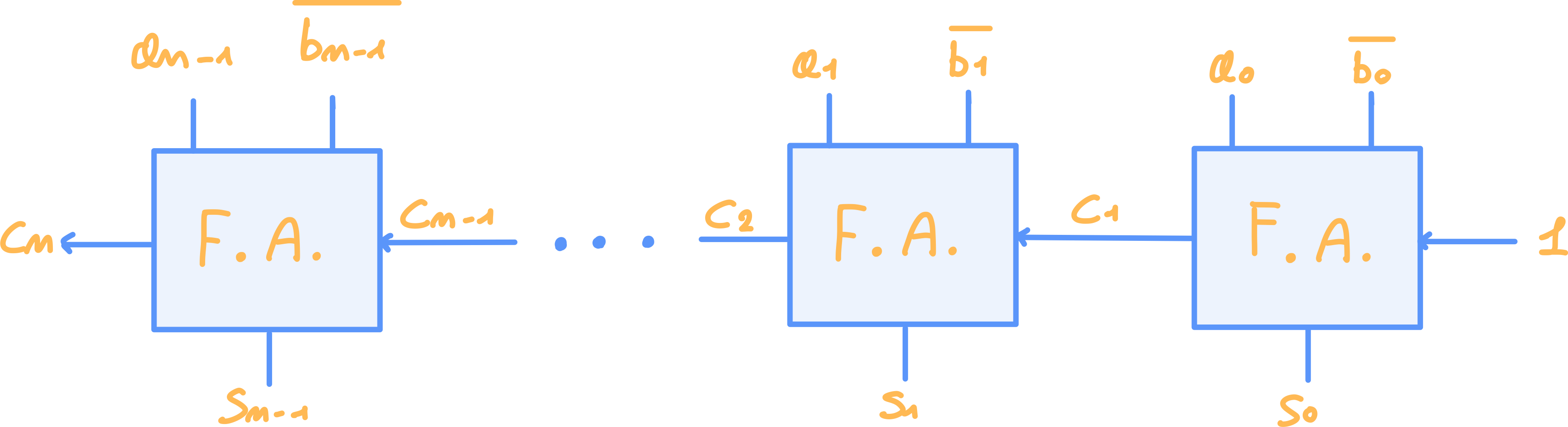
Circuito Sottrattore
Il Ripple Carry Adder può essere implementato per effettuare la sottrazione effettuando le stesse operazioni del Ripple Carry Adder ma:
- Negando ogni bit di
b - E dopo aver effettuato la somma, basta somma il risultato con
1per ottenere il giusto risultato in codifica CA2”
Problema (ritardo)
Il ripple carry adder, tuttavia, da il risultato dopo n cicli, poiché il Full-Adder deve aspettare il riporto del FA precedente.
Perciò eseguire un’ ulteriore somma raddoppierebbe il costo dal punto di vista temporale.
Per risolvere questa situazione, l’Half adder viene sostituito da un Full adder con riporto di ingresso pari a 1
Circuito
Circuito somma e sottrazione
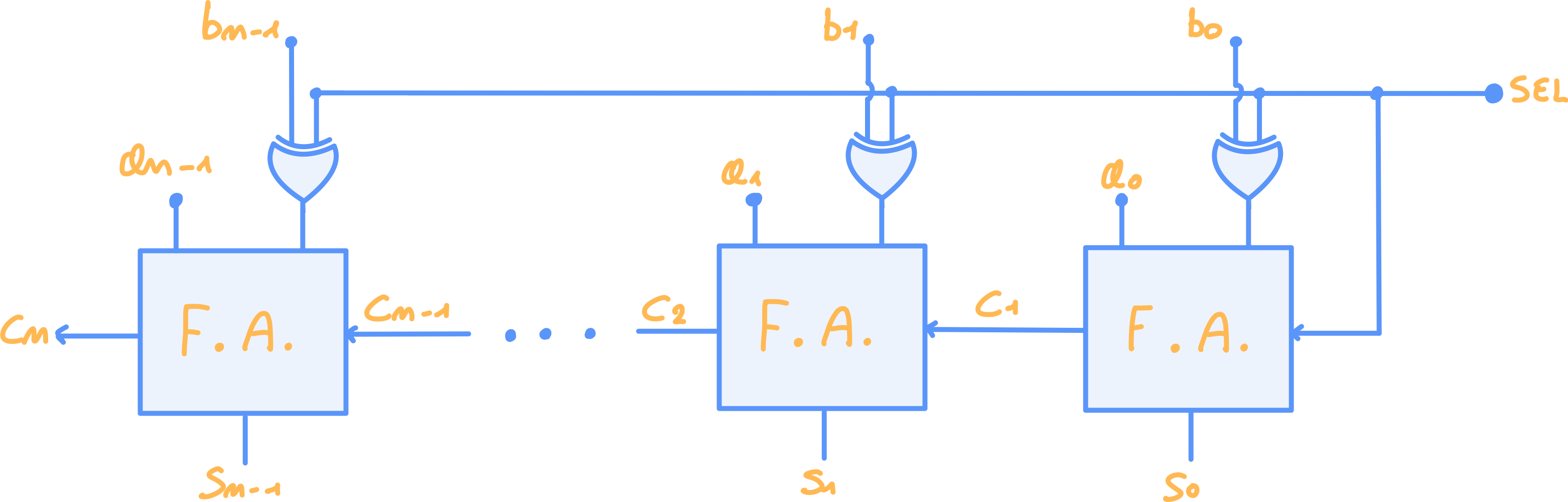
Le due operazioni possono essere combinate in un unico circuito attraverso un sistema di selezione formate da porte XOR connesse agli ingressi del secondo addendo (b). Il segnale di selezione (sel) controlla l’operazione da eseguire:
- sel = 0 ⇒ il circuito opera da sommatore.
- sel = 1 ⇒ il circuito opera da sottrattore.
Circuito
Funzionamento
- Quando Sel = 0 il circuito è in modalità somma, infatti i bit di B non vengono commentati e il primo full-adder riceve zero come carry.
- Quando Sel = 1 il circuito è in modalità sottrazione, infatti i bit di B vengono commentati e il primo full-adder riceve uno come carry