Proposizioni della Probabilità

Index

• 1° Probabilità dell’evento impossibile
• 2° Additività finita
• 3° Probabilità dell’evento complementare
• 4° Monotonia della funzione di probabilità
• 5° Somma probabilità di eventi non disgiunti

Related

• Studio delle Probabilità
• Calcolo delle Probabilità (class)

---

1° Probabilità dell’evento impossibile

La probabilità dell’evento impossibile è uguale a 0.

$$P(\varnothing )=0$$

Dimostrazione

Utilizzando l’assioma 3 dalla funzione di probabilità

Prendiamo la successione $E_1,E_2,E_3,...$ dove $E_1=\varnothing ,E_2=\varnothing ,E_3=\varnothing ,...,$ quindi abbiamo che $\forall i\ne j$ l’intersezione $E_i\cap E_j=\varnothing$.

Per l’assioma 3: $P\left({\bigcup }_{i=1}^{\infty }{E}_i\right)={\sum }_{i=1}^{\infty }P(E_i)$, quindi $P(\varnothing )={\sum }_{i=1}^{\infty }P(\varnothing )$

Per l’assioma 1 sappiamo che: $P(\varnothing )=[0,1]$.

Supponiamo che $P(\varnothing )\in (0,1]$ allora abbiamo che ${\sum }_{i=1}^{\infty }P(\varnothing )=+\infty$ e quindi $P(\varnothing )\ne {\sum }_{i=1}^{\infty }P(\varnothing )$, per esclusione abbiamo che $P(\varnothing )=0$ (altrimenti sarebbe $\infty$ che sappiamo essere impossibile perché max è 1)

---

2° Additività finita

Dati $n$ eventi a 2 a 2 incompatibili $E_1,E_2,\dots ,E_n$ vale che:

$$P\left(\bigcup _{i=1}^n{E}_i\right)=\sum _{i=1}^{n}P\left(E_i\right)$$

Esempio

• Domani piove con una probabilità 0.3
• Domani c’è il sole con una probabilità 0.6
• Domani nevica con una probabilità 0.1

Probabilità che piova o che nevichi = 0.3 + 0.1 = 0.4

Dimostrazione

Consideriamo la successione $F_1,F_2,\dots$ con:

$$F_1=E_1,F_2=E_2,\dots ,F_n=E_n,F_{n+1}=\varnothing ,F_{n+1}=\varnothing$$

Dato che la successione è fatta da eventi 2 a 2 incompatibili posso applicare il 3° assioma e otteniamo:

$$P\left(\bigcup _{i=1}^{\infty }{F}_i\right)=\sum _{i=1}^{\infty }P(F_i)$$

Che è equivalente a:

$$P\left(\bigcup _{i=1}^{\infty }{F}_i\right)=P(E_1)+P(E_2)+\cdots +P(E_n)+P(\varnothing )+\dots$$

Per la probabilità dell’evento impossibile abbiamo che $P(\varnothing )=0$ quindi tutti i $P(\varnothing )$ sono trascurabili, lasciando soltanto:

$$P\left(\bigcup _{i=1}^{\infty }{F}_i\right)=P(E_1)+P(E_2)+\cdots +P(E_n)$$

---

3° Probabilità dell’evento complementare

Consideriamo un evento $E$ la probabilità del suo evento complementare $E^c$ sarà:

$$P(E^c)=1-P(E)\forall E\subset S$$

Dimostrazione

$E$ e $E^c$ sono eventi incompatibili, quindi per l’additività finita abbiamo che:

$$P(E\cup E^c)=P(E)+P(E^c)$$

Ma sappiamo che $E\cup E^c=S$, quindi possiamo dire che $P(E\cup E^c)=P(S)=1$

Allora:

$$P(E)+P(E^c)=1⟹P(E^c)=1-P(E)$$

---

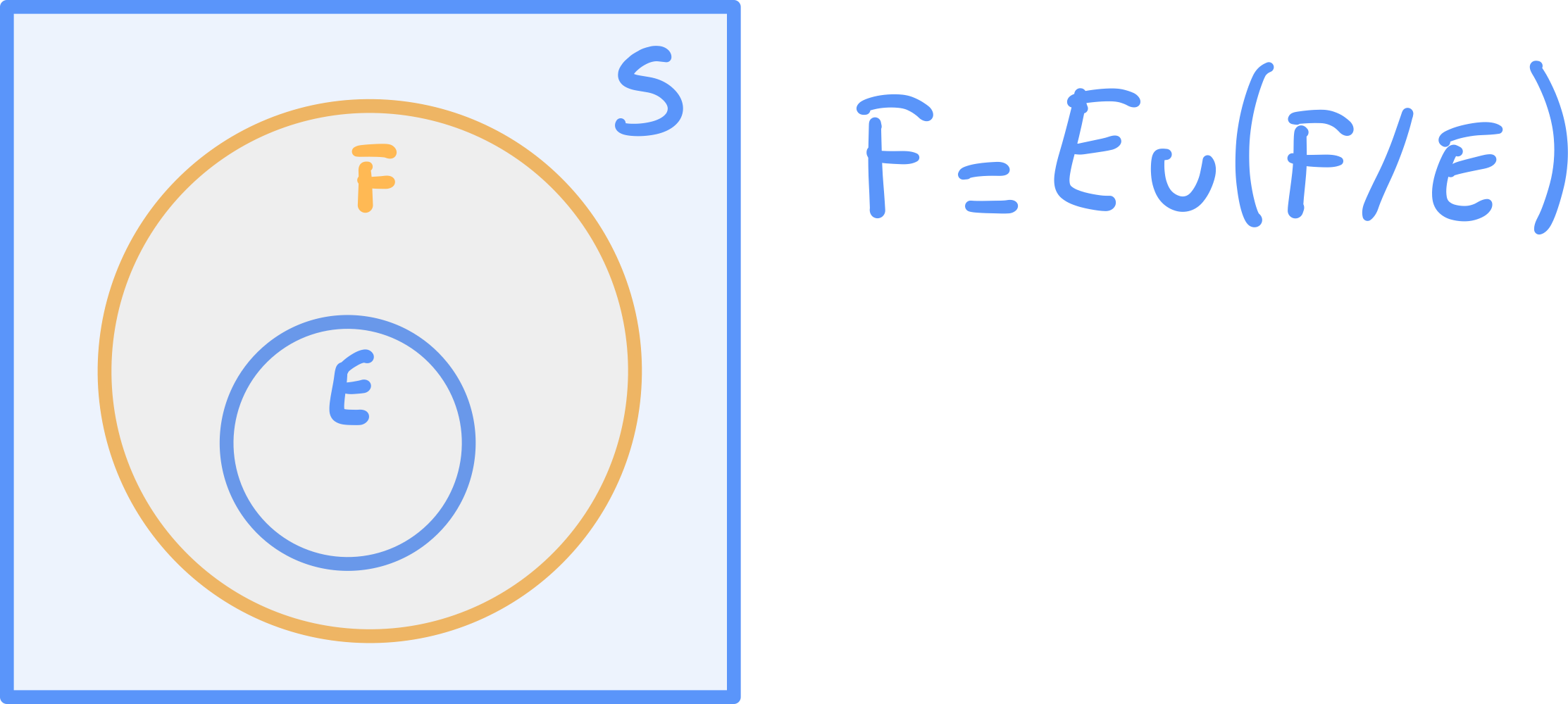
4° Monotonia della funzione di probabilità

Dati due eventi $F$ ed $E$ con $E\subset F$ vale che:

$$P(F)\le P(E)$$

Dimostrazione

$F=E\cup (F\setminus E)$, quindi $E$ ed $F\setminus E$ sono disgiunti.

Quindi, $P(F)=P(E)+P(F\setminus E)$ dato che per l’assioma 1 $P(F\setminus E)\ge 0$ allora $P(E)+P(F\setminus E)\ge P(E)$

---

5° Principio di Inclusione / Esclusione

$$\begin{array}{rl}& \text{Due Eventi:}P(A\cup B)=P(A)+P(B)-P(A\cap B)\\ & \\ & \text{Tre Eventi:}P(A\cup B\cup C)=P(A)+P(B)+P(C)-P(A\cap B)-P(A\cap C)-P(B\cap C)+P(A\cap B\cap C)\end{array}$$

Vedi: Principio di Inclusione ed Esclusione

Esempio

Giulia ha 2 libri, L1 e L2. L’evento E corrisponde a “Le piace L1” mentre F a “Le piace L2”. Sappiamo che:

• $P(E)=0,5$ (la probabilità che le piaccia L1 è del 50%)
• $P(F)=0,4$ (la probabilità che le piaccia L2 è del 40%)
• $P(E\cap F)=0,3$ (la probabilità che le piacciano entrambi è del 30%)

Vogliamo calcolare la probabilità che non le piaccia alcun libro. Per farlo, calcoliamo prima la probabilità che le piaccia almeno un libro, che è l’unione degli eventi E e F:

$$P(E\cup F)=P(E)+P(F)-P(E\cap F)$$

\geq 0,5 + 0,4 - 0,3 \geq 0,6

$$L^{\prime }eventocomplementaredi"Lepiacealmenounlibro"\grave{e}"Nonlepiacenessunlibro".Quindi,laprobabilit\grave{a}chenonlepiacciaalcunlibro\grave{e}:$$

P((E \cup F)’) = 1 - P(E \cup F) = 1 - 0,6 = 0,4

$$Quindi,laprobabilit\grave{a}chenonlepiacciaalcunlibro\grave{e}del40$$

---