Cardinalità ed equipollenza, insiemi finiti ed infiniti, numerabili ed innumerabili

---

Index

1. Cardinalità o potenza di un insieme

2. Equipotenza tra insiemi

3. Insieme finito ed infinito

4. Insiemi numerabili

5. Insiemi Continui

• Operazioni tra insiemi numerabili e innumerabili
• Insieme delle Parti e Numerabilità

Related

• Funzioni
• Matematica 0 (class)

---

Cardinalità o potenza di un insieme

🏗️ — da finire — 🏗️

---

Equipotenza tra insiemi

Definizione

Due insiemi A e B si dicono equipotenti se esiste una funzione biunivoca di dominio A e co-dominio B

Equipotenza tra insiemi finiti

Se A e B sono insiemi finiti allora sono equipollenti soltanto se hanno lo stesso numero di elementi.

---

Insieme finito ed infinito

Insieme finito

Un insieme si dice finito se non è equipotente ad alcun suo sottoinsieme proprio.

• Esempio:

&- \ \ \ \ A=\{1,2 \},\ \ B=\{1\} \ \ \ \textcolor{orange}{\text{oss: }B\subset A} \\ &-\ \ \ \ \text{Impossibile trovare funzione biettiva, quindi A è un insieme\textcolor{orange}{ finito}} \end{align}

Insieme infinito

Un insieme si dice infinito se è equipotente ad un suo sottoinsieme proprio

• Esempio: \begin{align} & - \ \ \ \ P = \{0,2,4,6,8,\dots\}\ \ \ \ \textcolor{orange}{\text{Insieme numeri pari positivi}} \\ & - \ \ \ \ I = \{2,4,6,8,10,\dots\}\ \ \ \textcolor{orange}{\text{Insieme numeri pari positivi diversi da 0}} \\ \\ & \ \ \ \ \ \ \ \ \ \textcolor{orange}{\text{oss: }} I\subset P \\ \\ & - \ \ \ \ f:P\to I\ \ \ t.c. \ \ \ f(x)=x+2 \ \ \ \ \textcolor{orange}{\text{Funzione biettiva}} \\ & - \ \ \ \ f^{-1}(x)=x-2 \\ \\ & \underline{\text{Quindi P ed I sono \textcolor{orange}{equipotenti} e P è \textcolor{orange}{infinito}} } \\ \\ &\ \ \ \ P\ =\ \ 0\ \ \ \ 2\ \ \ \ 4\ \ \ \ 6\ \ \ \ 8\ \ \ \ \dots \\ &\ \ \ \ f :\ \ \ \ \ \ |\ \ \ \ \ |\ \ \ \ \ |\ \ \ \ \ |\ \ \ \ \ |\ \ \ \ \dots \\ &\ \ \ \ I\ =\ \ \ 2\ \ \ \ 4\ \ \ \ 6\ \ \ \ 8\ \ \ 10\ \ \ \dots \end{align}

---

Insiemi numerabili

$$\text{Un insieme A si dice numerabile se e soltanto se esiste una corrispondenza biunivoca tra A e }\mathbb{N}$$

Insieme interi numerabile

$l$

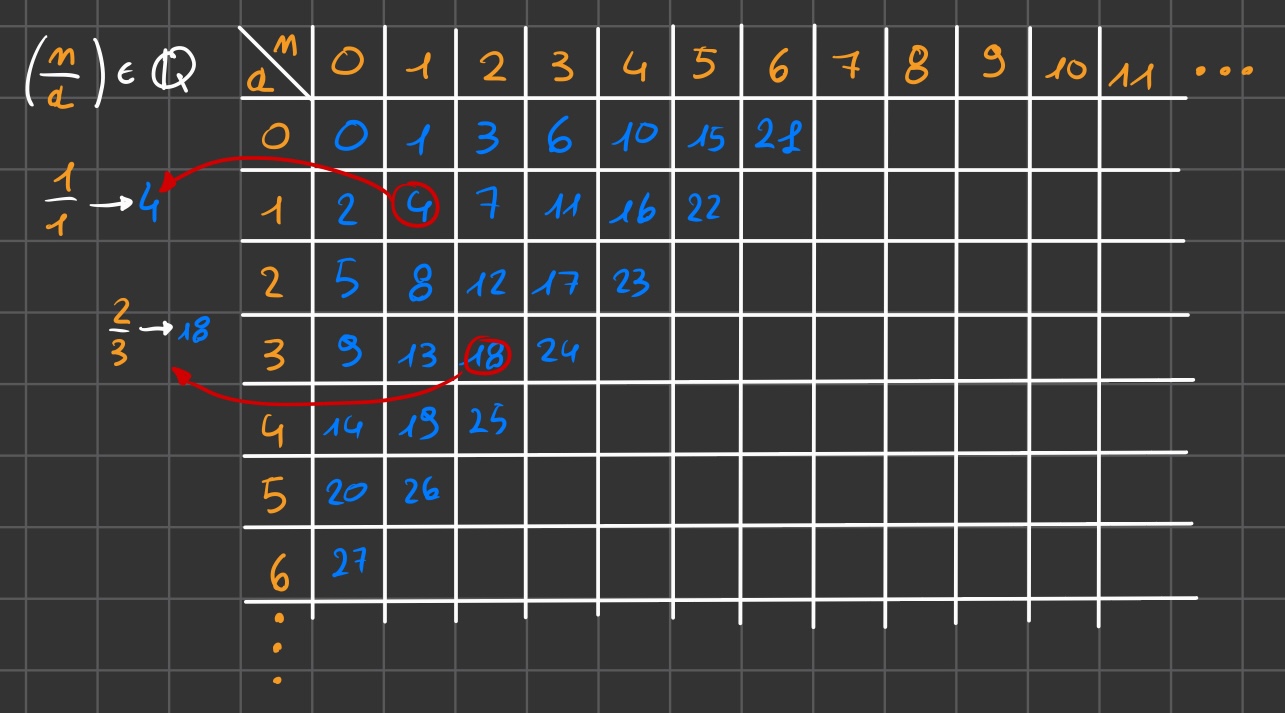
Insieme razionali numerabile

Vedi:

• Tecnica della diagonale di Cantor 🔴
• https://it.m.wikipedia.org/wiki/Argomento_diagonale_di_Cantor

---

Insiemi Continui

oss: insieme delle parti di N è equipotente a R (continuo)

N. pari 0° ⇒ 0 1° ⇒ 2 2° ⇒ 4

2n