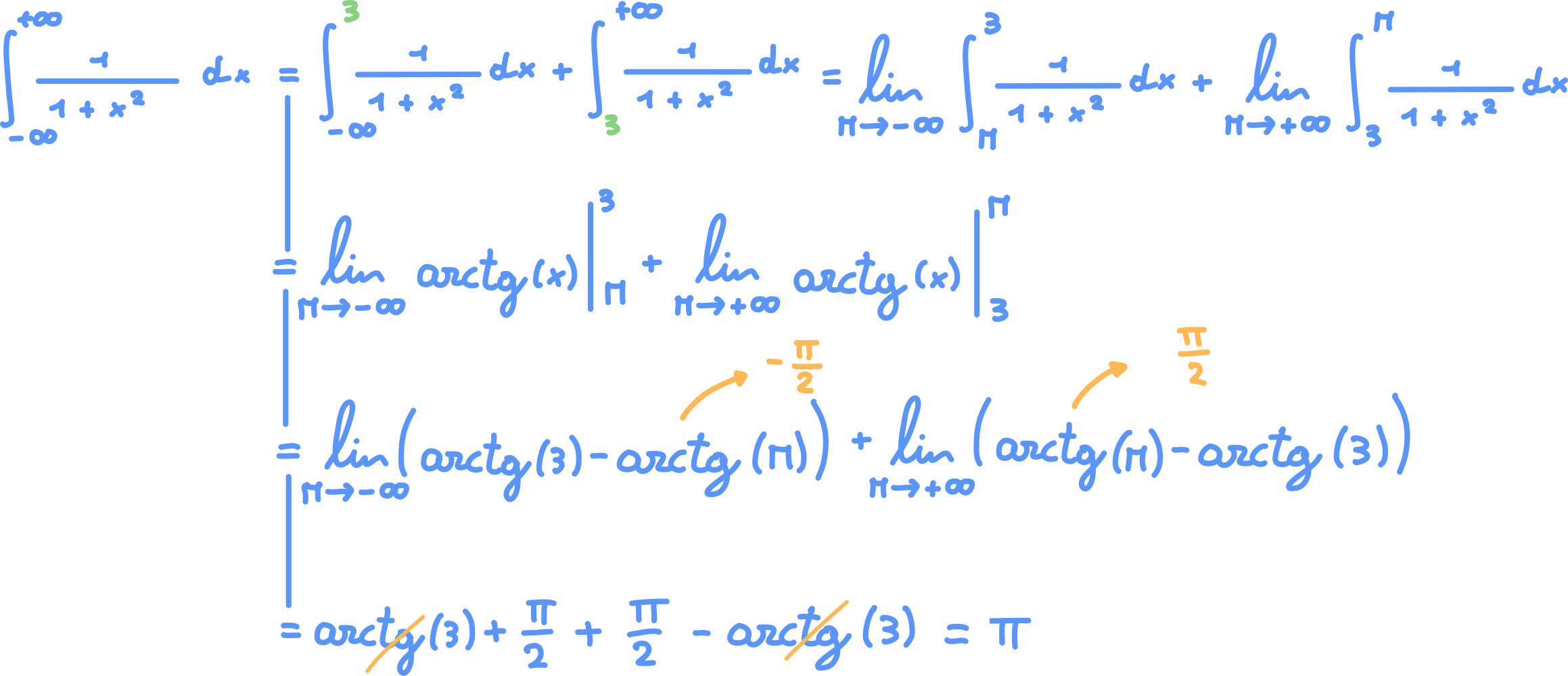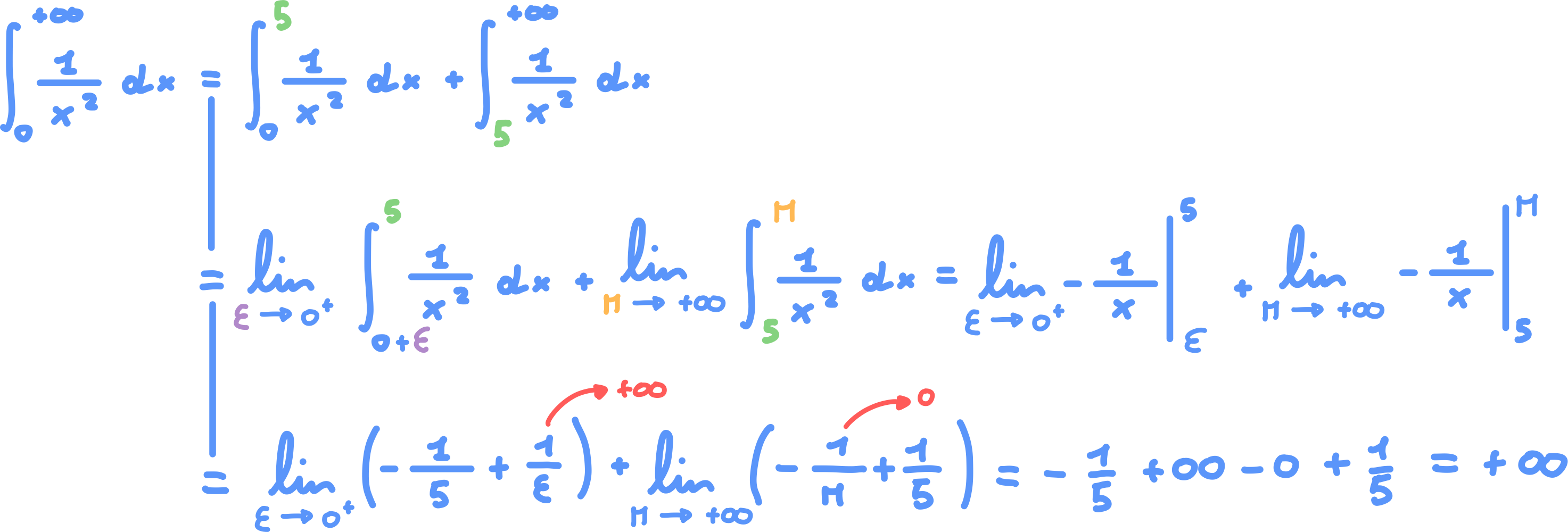Introduzione (integrali impropri)

---

Index

1. Cos’è un Integrale Improprio
2. Integrali di Funzioni Illimitate
3. Integrali con zona di integrazione illimitata
4. Esempi

Related

• Integrali
• Integrali Impropri
• Calcolo Integrale (class)
• Esercizi Integrali Impropri

---

Cos’è un Integrale Improprio

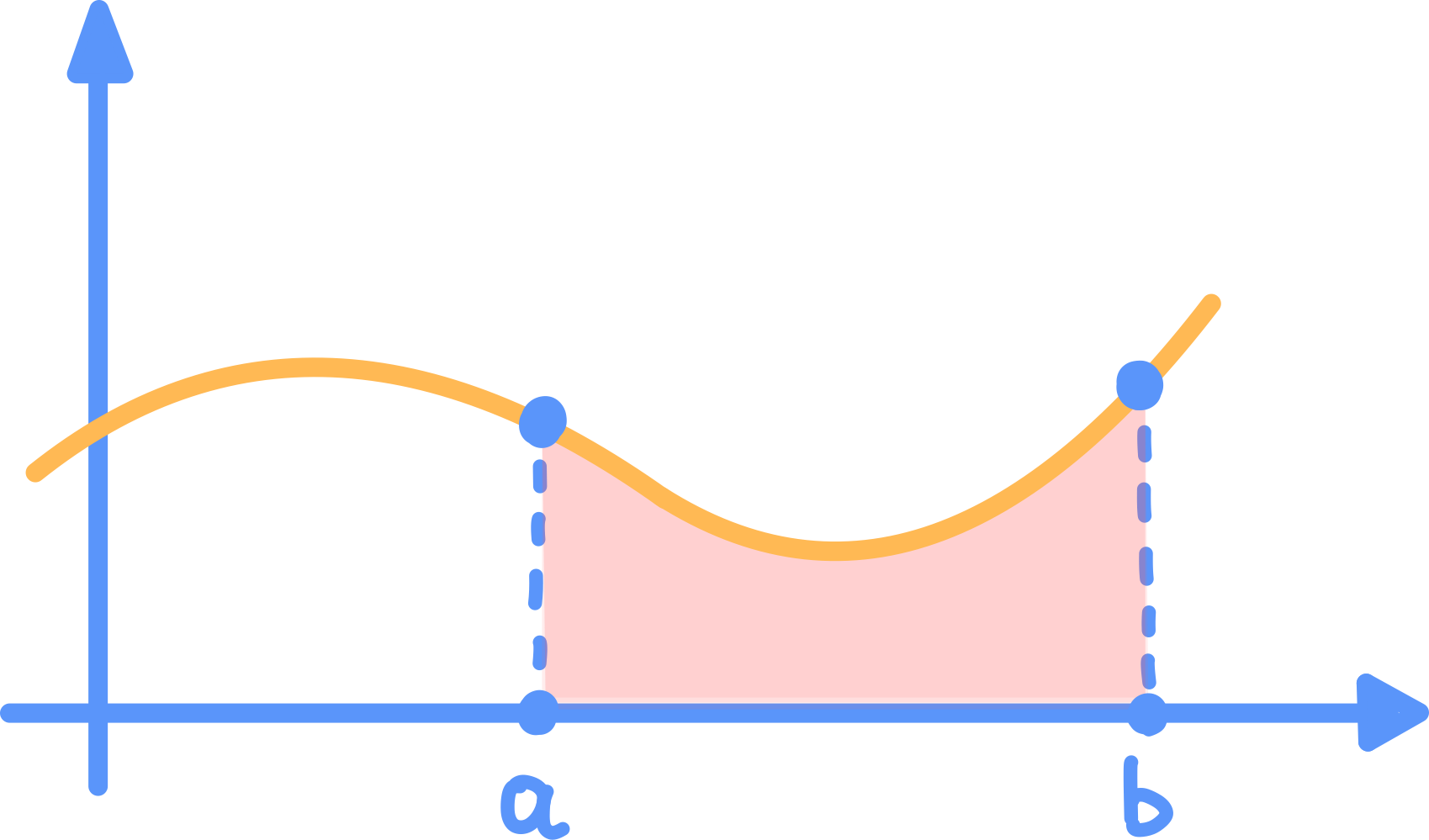
Integrali Propri

Gli integrali visti fino ad ora sono integrali propri, dove:

• La zona di integrazione è limitata.
• La funzione integranda è limitata.

Se una di queste due proprietà viene meno allora si parla di Integrale Improprio.

Integrale Improprio

Sia $f(x)$ una funzione di discontinuità illimitata nel punto $x=b$, allora:

$${\int }_a^{b}f(x)dx=\text{ Non Integrabile Secondo Rienmann}$$

Allora, $f(x)$ si dice integrabile in senso improprio in $[a,b]$ se l’integrale per $[a,b-ϵ]$ dove $ϵ\to 0^{+}$ ammette limite finito:

$$\underset{ϵ\to 0^{+}}{\lim }{\int }_a^{b-ϵ}f(x)dx=\underset{ϵ\to 0^{+}}{\lim }F(x){|}_a^{b-ϵ}=\ell$$

Dove:

• $\ell$ è un numero finito
• $F(x)$ è una primitiva di $f(x)$

---

Integrali di Funzioni Illimitate

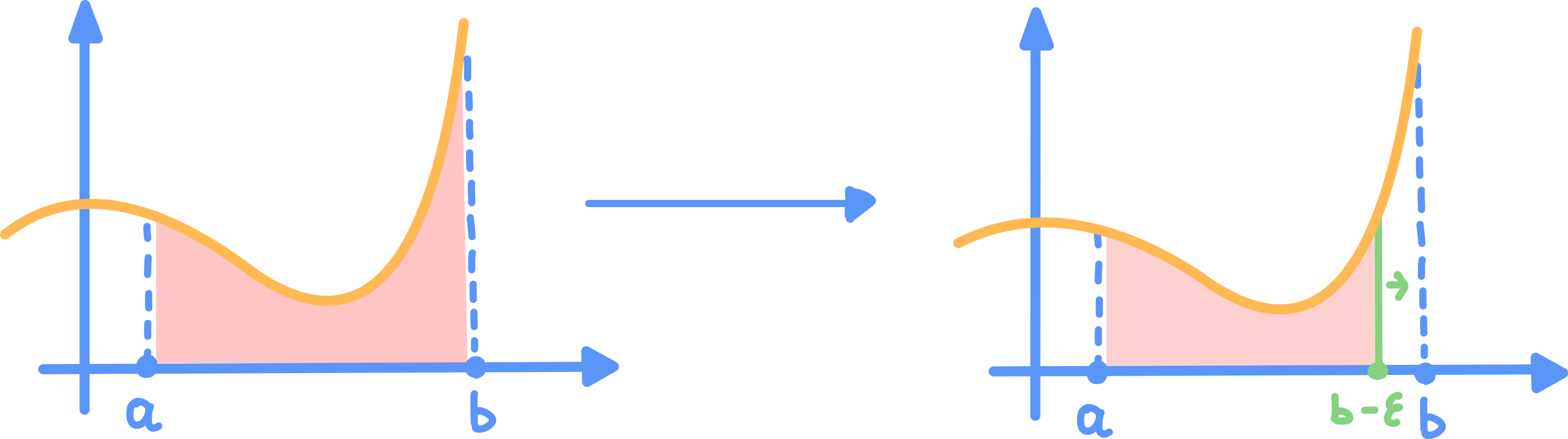
Funzione illimitata sull'Estremo Destro

Sia $f(x):[a,b)\to \mathbb{R}$ continue e illimitata sull’estremo destro (ovvero ${\lim }_{x\to b^{-}}f(x)=\pm \infty$)

• In questo caso di definisce:

$${\int }_a^{b}f(x)dx=\underset{ϵ\to 0^{+}}{\lim }\boxed{{\int }_a^{b-ϵ}f(x)dx}(\text{Integrale Proprio})$$

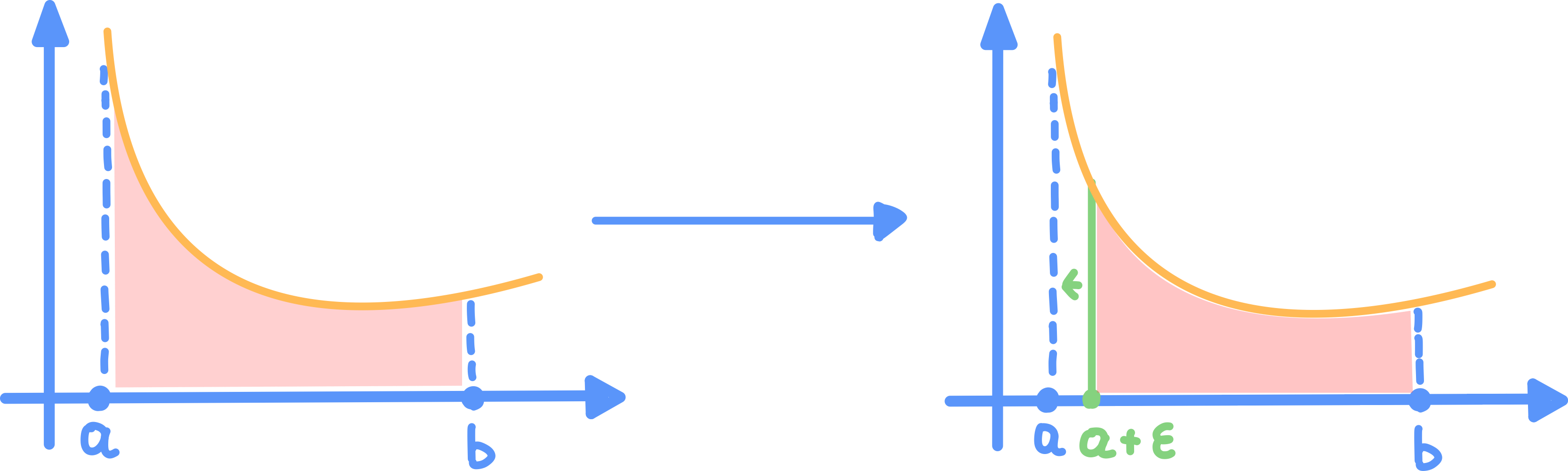
Funzione illimitata sull'Estremo Sinistro

Sia $f(x):(a,b]\to \mathbb{R}$ continue e illimitata sull’estremo sinistro (ovvero ${\lim }_{x\to a^{+}}f(x)=\pm \infty$)

• In questo caso di definisce:

$${\int }_a^{b}f(x)dx=\underset{ϵ\to 0^{+}}{\lim }\boxed{{\int }_{a+ϵ}^{b}f(x)dx}(\text{Integrale Proprio})$$

Converge, Diverge o Indeterminato

In entrambi i casi, se il limite:

• Esiste ed è finito, allora $f(x)$ si dice integrabile in $[a,b]$ o che ${\int }_a^{b}f(x)dx$ converge.
• Risulta $\pm \infty$, allora si dice che l’integrale proprio diverge.
• Non esiste, allora si dice che l’integrale improprio è indeterminato.

Esempio

$${\int }_0^4\frac{1}{2\sqrt{x}}dx=\underset{ϵ\to 0^{+}}{\lim }\int \frac{1}{2\sqrt{x}}dx=\underset{ϵ\to 0^{+}}{\lim }\sqrt{x}{|}_{ϵ}^4=\underset{ϵ\to 0^{+}}{\lim }(\sqrt{4}-\sqrt{ϵ})=2-0=2$$

---

Integrali con zona di integrazione illimitata

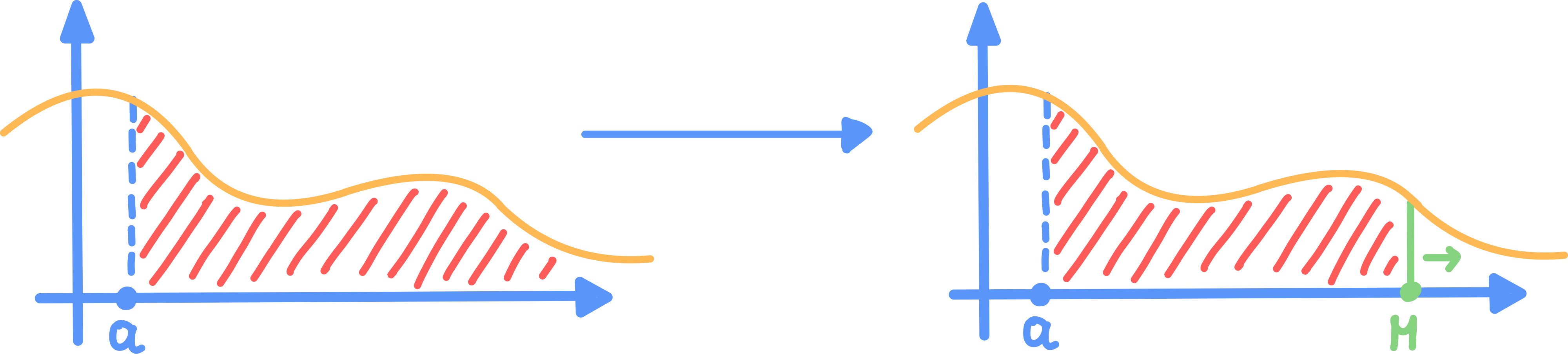
Zona di integrazione illimitata a destra

Sia $f:[a,+\infty ]\to \mathbb{R}$ una funzione continua:

• In questo caso si definisce:

$${\int }_a^{+\infty }f(x)dx=\underset{M\to +\infty }{\lim }{\int }_a^{M}f(x)dx$$

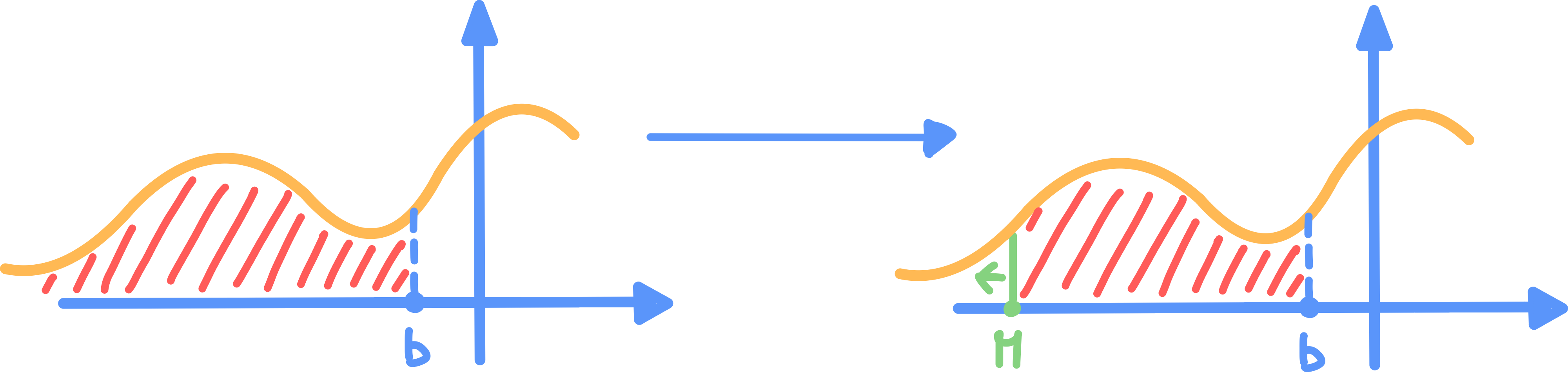
Zona di integrazione illimitata a sinistra

Sia $f:(-\infty ,b)\to \mathbb{R}$ una funzione continua:

• In questo caso si definisce:

$${\int }_{-\infty }^{b}f(x)dx=\underset{M\to -\infty }{\lim }{\int }_M^{b}f(x)dx$$

Esempio

$${\int }_4^{+\infty }\frac{1}{x^2}dx=\underset{M\to +\infty }{\lim }-\frac{1}{x}{|}_4^M=\underset{M\to +\infty }{\lim }(-\frac{1}{M}+\frac{1}{4})=0+\frac{1}{4}=\frac{1}{4}$$

---

Integrale Improprio con più problemi

Un integrale improprio può essere suddiviso in più problemi da risolvere.

Infatti è molto comune incontrare integrali che hanno entrambi gli estremi degli intervalli divergenti e che allo stesso momento hanno anche la funzione che diverge in determinati punti.

Metodo

In questi casi si deve:

1. Spezzare l’integrale in più integrali aventi un singolo problema
2. Risolvere i singoli integrali
3. Dedurre il comportamento dell’integrale “globale” sommando i risultati dei vari pezzi.

Esempi

Esercizio 2.

Integrale improprio con intervallo di integrazione illimitato sia a sinistra che a destra.

Link to original

Esercizio 3.

$${\int }_0^{+\infty }\frac{1}{x^2}dx$$

Integrale improprio con:

• Intervallo di integrazione illimitato a destra
• Funzione illimitata su 0 (sinistra)

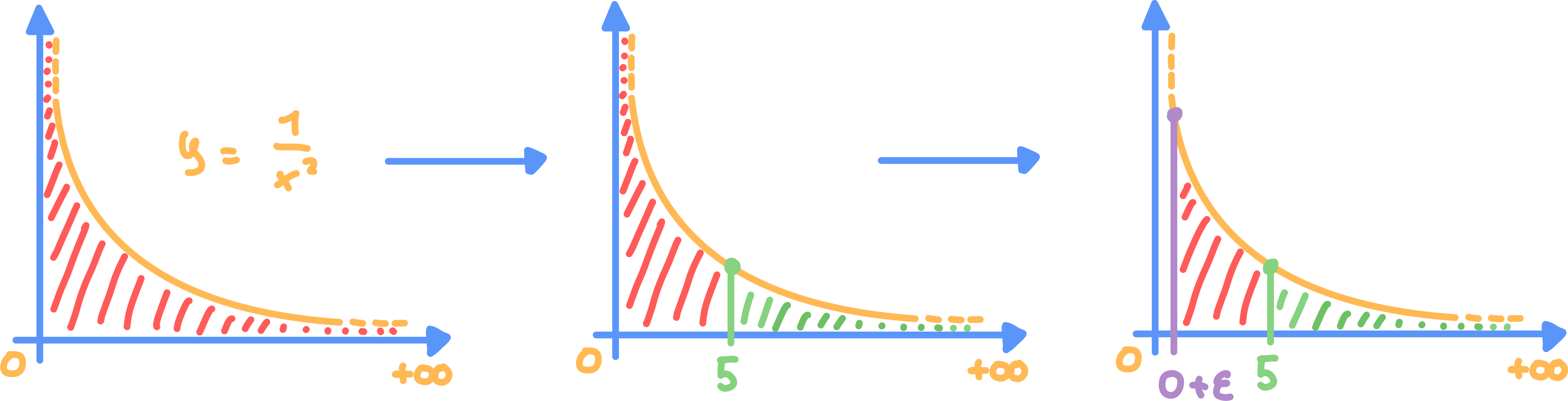
Risoluzione:

Grafico funzione:

Link to original