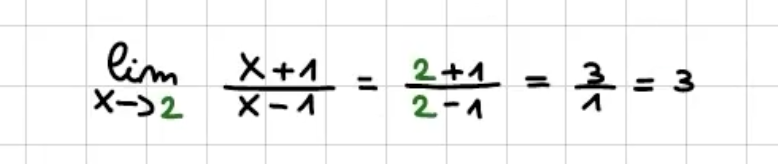Limiti di Funzioni Razionali

Index

1. Definizione
2. Limite di funzione razionale con x ⇒xo
3. Limite di funzione razionale con x ⇒∞

Related

• Limiti
• Calcolo Differenziale (class)

---

Definizione

Un limite di una funzione razionale non è altro che, un limite di una frazione che presenta al numeratore o al denominatore un incognita

---

Limite di funzione razionale con x ⇒xo

Un limite di una frazione che presenta al numeratore o al denominatore un incognita che tende ad un valore finito. ${\lim }_{n\to x_0}\frac{N(x)}{D(x)}$

Metodo Risolutivo

1. Sostituisco le x della funzione con x0
2. Risolvo la funzione

• Esisto 4 possibili casistiche:

  1. non si annullano ne il numeratore ne il denominatore

  2. si annulla il numeratore ma non il denominatore

  3. si annulla il denominatore ma non il numeratore:

  4. si annulla sia il denominatore sia il numeratore

Caso 1) non si annullano ne il numeratore ne il denominatore

Il limite esiste e la funzione è continua

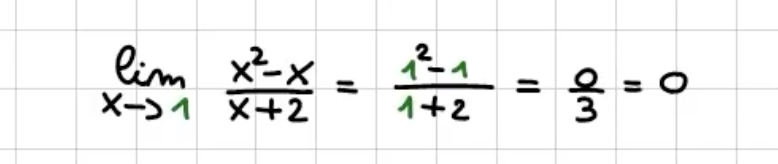
Caso 2) si annulla il numeratore ma non il denominatore

Il limite esiste e la funzione è continua

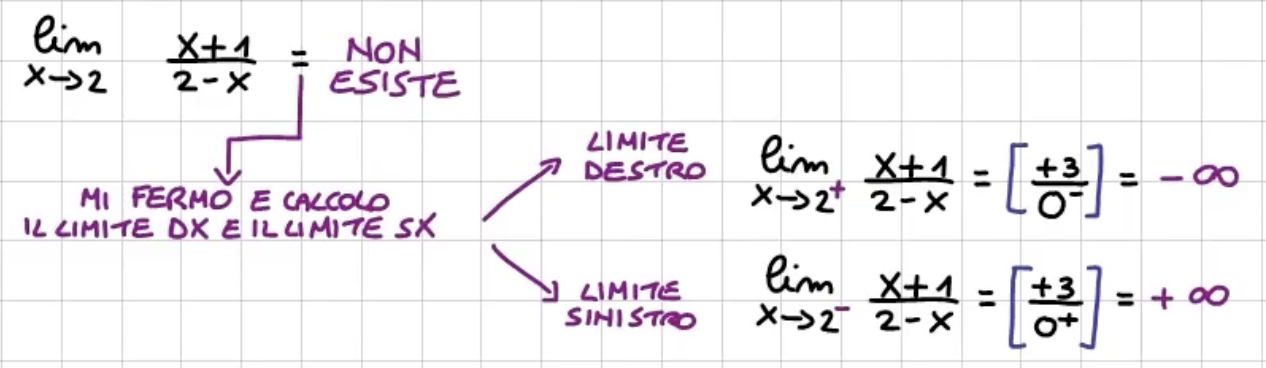
Caso 3) si annulla il denominatore ma non il numeratore

Si fa limite destro e sinistro della funzione

• Se limite destro e sinistro non congruenti, il limite non esiste (asintoto verticale)

• Se limite destro e sinistro congruenti, il limite esiste

Caso 4) si annulla sia il denominatore sia il numeratore

oss: Forma indeterminata $\frac{0}{0}$

Utilizzare metodo scomporre e semplificare

---

Limite di funzione razionale con x ⇒∞

Un limite di una frazione che presenta al numeratore o al denominatore un incognita che tende ad +- ∞

$$\underset{n\to \pm \infty }{\lim }\frac{N(x)}{D(x)}$$

Metodo Risolutivo

1. Raccogliere il grado massimo al numeratore e al denominatore (come per Limiti di Funzioni Polinomiali)

2. Semplificare

3. Guardare a cosa tendono i termini superstiti

Esempi

Osservazioni

• Se numeratore è di grado maggiore rispetto al denominatore il risultato sarà ∞.
• Se numeratore è di grado inferiore rispetto al denominatore il risultato sarà 0.
• Se numeratore e denominatore anno lo stesso grado il risultato sarà un numero finito.