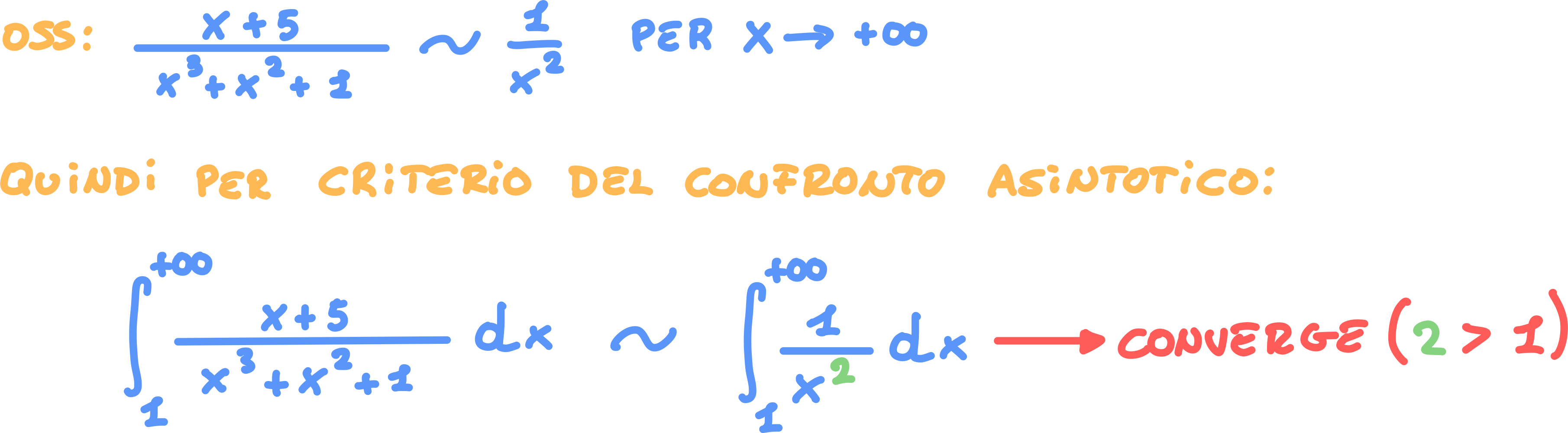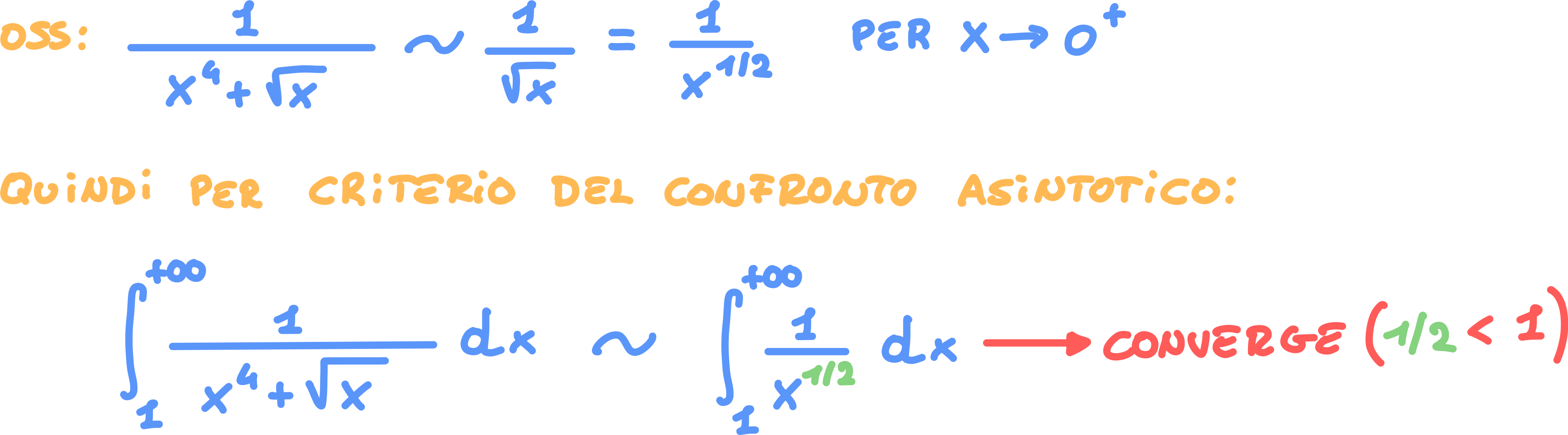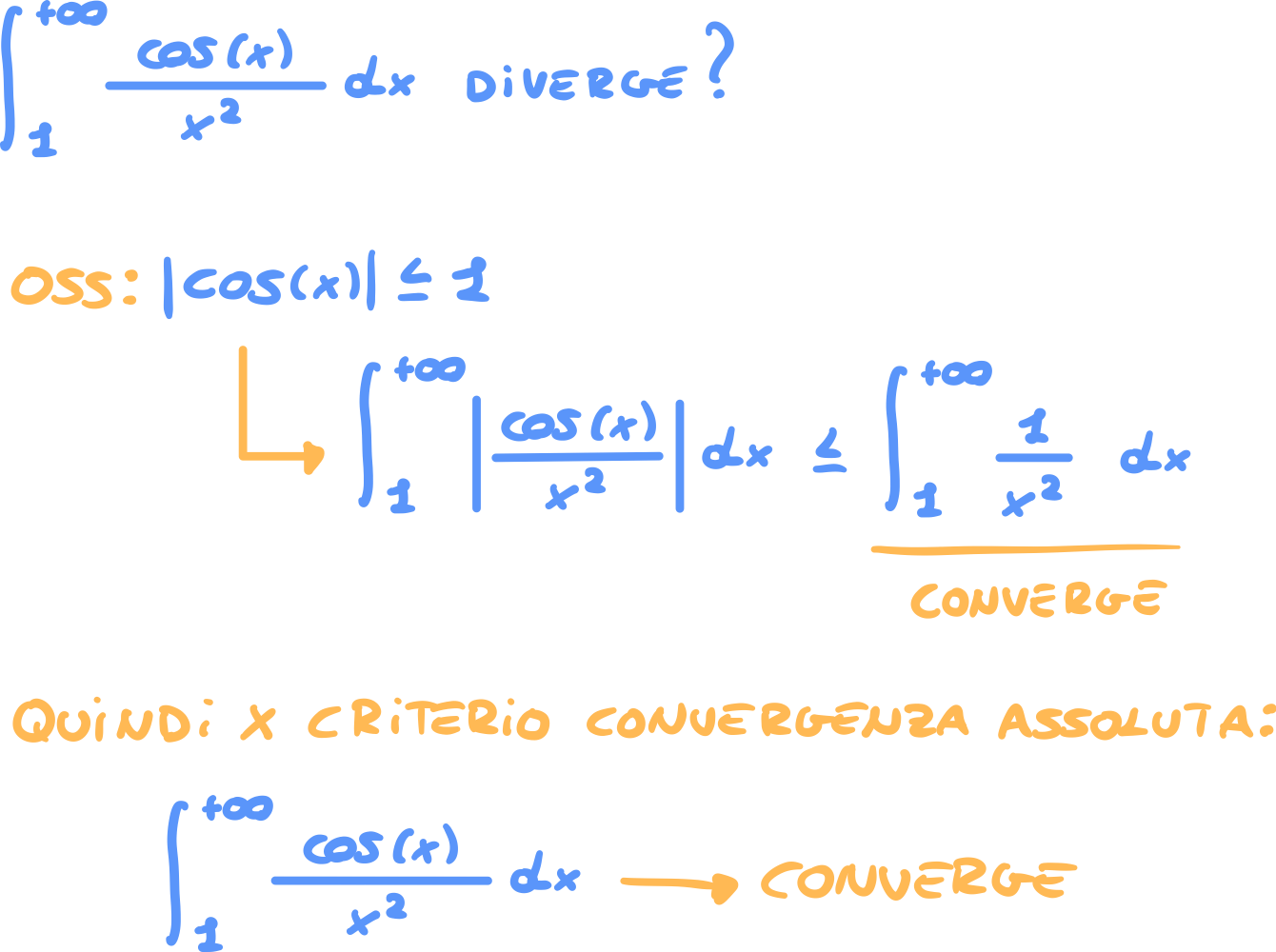Criteri di Convergenza (integrali impropri)

---

Index

1. Criterio Confronto Asintotico
2. Criterio Confronto
3. Esempi

Related

• Integrali
• Integrali Impropri
• Calcolo Integrale (class)

---

Criterio Confronto Asintotico

Zona di Integrazione Illimitata

Siano $f,g:[a,+\infty )\to \mathbb{R}$ due funzioni continue e positive:

$$\underset{x\to x_0}{\lim }\frac{f(x)}{g(x)}=\ell ⟹{\int }_a^{+\infty }f(x)dx\sim {\int }_a^{+\infty }g(x)dx$$

Quindi sappiamo che:

• Se ${\int }_a^{+\infty }g(x)dx$ converge, allora ${\int }_a^{+\infty }f(x)dx$ converge
• Se ${\int }_a^{+\infty }g(x)dx$ diverge, allora ${\int }_a^{+\infty }f(x)dx$ diverge

Funzione Illimitata

Siano $f(x)$ e $g(x)$ due funzioni, continue e positive, tali che in $x_0$ vi sia un punto illimitato e $\ell \in (0,+\infty )$, allora:

$$\underset{x\to x_0}{\lim }\frac{f(x)}{g(x)}=\ell ⟹{\int }_a^{x_0}f(x)dx\sim {\int }_a^{x_0}g(x)dx$$

Quindi sappiamo che:

• Se ${\int }_a^{x_0}g(x)dx$ converge, allora ${\int }_a^{x_0}f(x)dx$ converge
• Se ${\int }_a^{x_0}g(x)dx$ diverge, allora ${\int }_a^{x_0}f(x)dx$ diverge

oss: analogo al Criterio del confronto asintotico (Serie)

---

Criterio Confronto

Zona di Integrazione Illimitata

Siano $f,g:[a,+\infty )\to \mathbb{R}$ due funzioni, se:

$$0\le f(x)\le g(x)\text{in }[a,+\infty )$$

Allora sappiamo che:

• Se ${\int }_a^{+\infty }g(x)dx$ converge, allora ${\int }_a^{+\infty }f(x)dx$ converge
• Se ${\int }_a^{+\infty }f(x)dx$ diverge, allora ${\int }_a^{+\infty }g(x)dx$ diverge

Funzione Illimitata

Siano $f(x)$ e $g(x)$ due funzioni tali che in $x_0$ vi sia un punto illimitato, se:

$$0\le f(x)\le g(x)\text{in }[a,x_0)$$

Allora sappiamo che:

• Se ${\int }_a^{x_0}g(x)dx$ converge, allora ${\int }_a^{x_0}f(x)dx$ converge
• Se ${\int }_a^{x_0}f(x)dx$ diverge, allora ${\int }_a^{x_0}g(x)dx$ diverge

oss: analogo al Criterio del confronto (Gauss - Serie)

---

Criterio Convergenza Assoluta

Zona di Integrazione Illimitata

Sia $f:[a,+\infty )\to \mathbb{R}$ una funzione integrabile su $[a,+\infty )$, allora:

$$\text{Se }{\int }_a^{+\infty }|f(x)|dx\text{converge}⟹{\int }_a^{+\infty }f(x)dx\text{converge}$$

Funzione Illimitata

Sia $f(x)$ una funzione tale che in $x_0$ vi sia un punto illimitato, allora:

$${\int }_a^{x_0}|f(x)|dx\text{converge}⟹{\int }_a^{x_0}f(x)dx\text{converge}$$

oss: analogo al Criterio della convergenza assoluta (Serie)

---

Esercizi con criteri di convergenza

Esercizio 1. (confronto)

Integrali con intervallo illimitato a destra:

• Stabilire se ${\int }_1^{+\infty }{e}^{-x^2}dx$ converge.

Soluzione:

Esercizio 2. (confronto asintotico)

Integrali con intervallo illimitato a destra:

• Stabilire se ${\int }_1^{+\infty }\frac{x+5}{x^3+x^2+1}dx$ converge.

Soluzione:

Esercizio 3. (confronto asintotico)

Integrale con funzione divergente in $x=0$

• Stabilire se ${\int }_0^2\frac{1}{x^4+\sqrt{x}}dx$ converge

Soluzione:

Esercizio 4. (convergenza assoluta)

Link to original

^37ec46