Funzioni Continue

Index

1. Funzione continua in un punto
2. Funzione continua su un intervallo
3. Calcolare se funzione è continua in un punto
4. Calcolare se funzione è continua in un intervallo

Related

• Funzioni
• Calcolo Differenziale (class)

---

Funzione continua in un punto

Sia:

• $f:[a,b]\to \mathbb{R}$
• $x_0\in [a,b]$

Si dice che la funzione f(x) è continua in x0 se: $\boxed{\underset{x\to x_0}{\lim }f(x)=f(x_0)}$

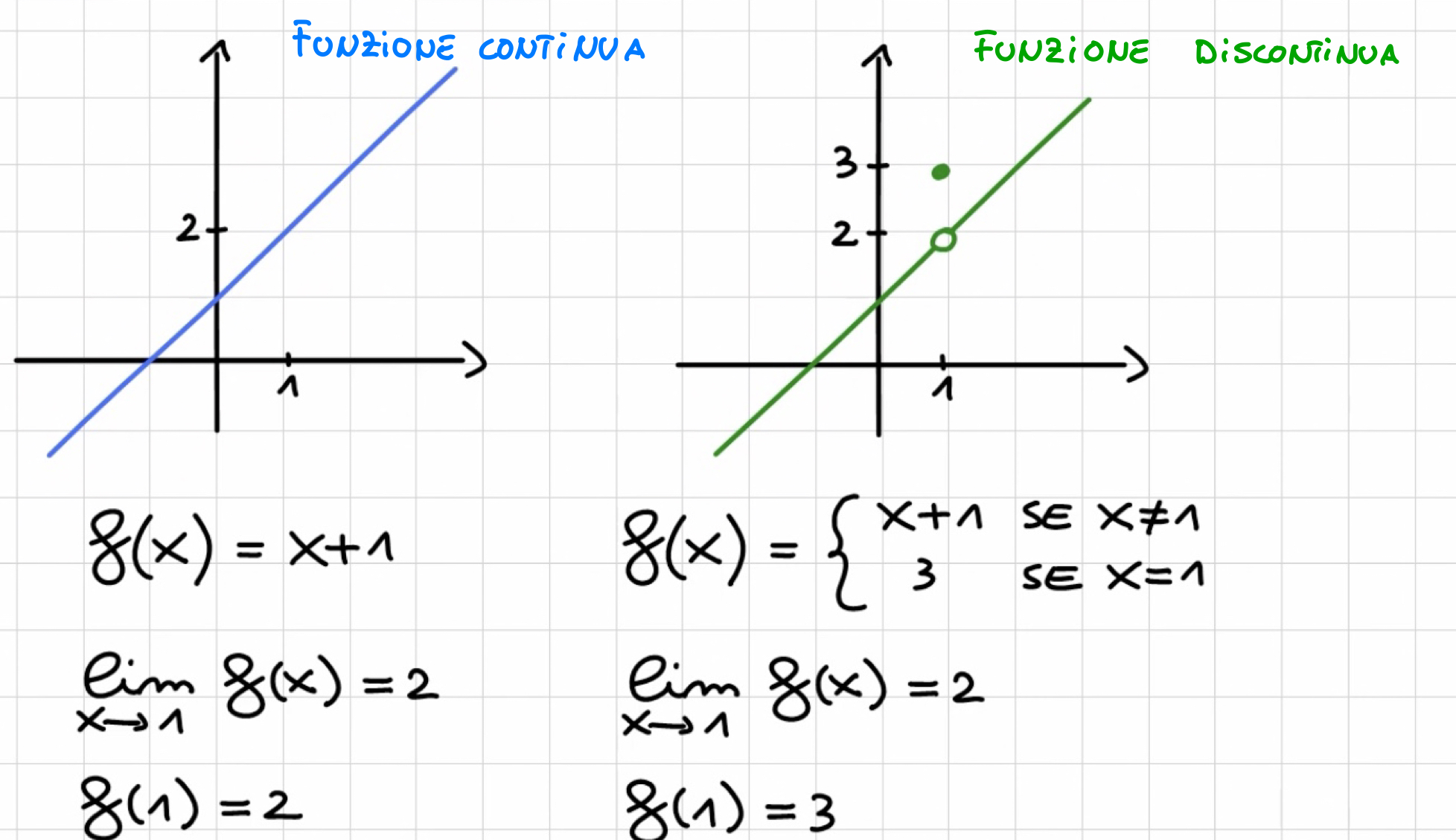
Esempio

---

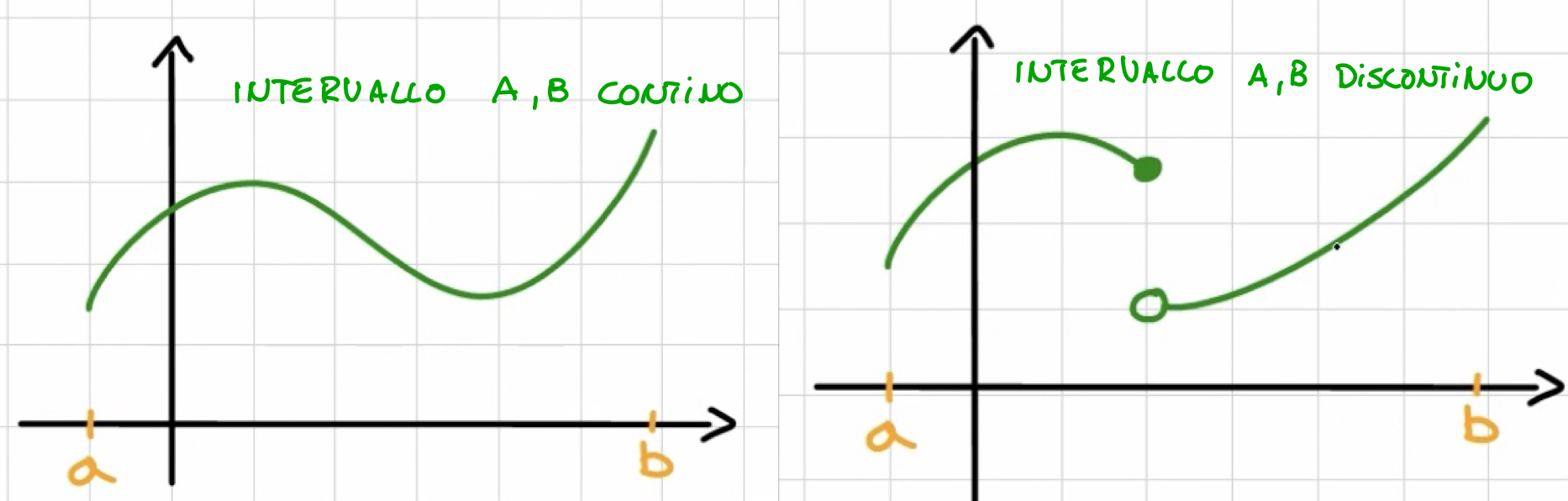
Funzione continua su un intervallo

Una funzione $f:[a,b]\to \mathbb{R}$ si dice continua in $[a,b]$ se è continua in $x_0$, $\forall x_0\in [a,b]$

---

Calcolare se funzione è continua in un punto

Definizione

f è continua in $x_0$ se esiste sia limite destro che sinistro e sono coincidenti

$$\begin{array}{rl}& 1.\exists \underset{n\to {x_0}^{+}}{\lim }f(x)=L^{+}\\ & 2.\exists \underset{n\to {x_0}^{-}}{\lim }f(x)=L^{-}\\ & 3.L^{-}=L^{+}=f(x_0)\end{array}$$

Esempio 1

3x+2 &x\geq 0 \\ \frac{sen(2x)}{x} & x<0 \end{cases}$$ Calcolare se $f$ è continua in $x_{0}=0$ 1) $L^{+} = \underset{ x\to {{0}^{+}} }{ \lim } f(x)=\underset{ n \to 0^+ }{ \lim } (3x+2)=3 \cdot 0 +2=\textcolor{orange}2$ 2) $L^{-}=\underset{ { n \to 0^- } }{ \lim } f(x)= \underset{ n \to 0^- }{ \lim } \frac{sen(2x)}{x}=\underset{ n \to 0^- }{ \lim } \frac{2x}{x} = \underset{ n \to 0^- }{ \lim }2 =\textcolor{orange}2$ 3) $f(0) = 3\cdot 0+2=\textcolor{orange}2$ 4) $L^{+}=L^{-}=f(0)$ Quindi $f$ è continua in $x_{0}=0$

Esempio 2

\frac{e^{3x}-1}{x} &x\geq 0 \\ a &x = 0 \\ \frac{tg^{2}(bx)}{x^{2}} & x<0 \\ \end{cases}$$ Calcolare $a,b \in \mathbb{R}$ tali che $f$ è continua in $x_{0}=0$ 1) $L^{+} = \underset{ x\to {{0}^{+}} }{ \lim } f(x)=\underset{ n \to 0^+ }{ \lim } \frac{tg^{2}(bx)}{x^{2}} = \frac{(bx)^{2}}{x^{2}} =\textcolor{orange}{b^{2}}$ 2) $L^{-}=\underset{ { n \to 0^- } }{ \lim } f(x)= \underset{ n \to 0^- }{ \lim } \frac{e^{3x}-1}{x}=\underset{ n \to 0^- }{ \lim } \frac{3x}{x} =\textcolor{orange}3$ Quindi $\underset{ x\to 0 }{ \lim } f(x)$ esiste $\iff\ L^{+} = L^{-} \implies \boxed{b^{2}=3}\implies \boxed{b= \pm \sqrt[2]{3}}$

Se $b^2=3$

• allora $\underset{x\to 0}{\lim }f(x)=3=a=f(0)$
• Quindi $L^{+}=L^{-}=f(0)=3$

Risultato $f$ è continua in $x_0=0$ se $a=3$ e $b^2=3$

---

Calcolare se funzione è continua in un intervallo

Definizione

$f[a,b]\to \mathbb{R}$ è continua in $[a,b]$ se f è continua in $x_0,\forall x_0\in [a,b]$

Esempio

Determinare $a,b\in \mathbb{R}$ tali che $f(x)$ sia continua in $\mathbb{R}$

\begin{cases} \frac{\sin(ax)}{x} &se\ \ x>0 \\ x^{2}+b & se\ \ x\leq 0 \\ \end{cases}$$ >[!warning] $\frac{\sin (ax)}{x}$ con $x>0$: >Se $x>0$ allora: $\frac{\sin(ax)}{x}$ è una funzione continua >- Infatti una divisione tra due funzioni continue è una funzione continua ([[Operazioni tra funzioni continue|read]]) >[!warning] $x^{2}+b$ con $x<0$: >Se $x<0$, $x^{2}+b$ è una funzione continua $\forall b$ >- Infatti $x^{2}+b$ è un polinomio >[!warning] $\frac{\sin (ax)}{x}$ con $x\to 0^{+}$: >$$ \begin{align} > & \lim_{ n \to 0 }= f(0) = 0^{2}+b=\boxed{b} \\ > & \ \ \ \ \ \ \ - \lim_{ n \to 0^{-} } f(x)=\lim_{ n \to 0^{-}}{(x^{2}+b)}=\boxed{b }\\ > & \ \ \ \ \ \ \ - \lim_{ n \to 0^{+} } f(x)=\lim_{ n \to 0^{+}}{\frac{\sin(ax)}{x}}=\boxed{a}\\ \\ > & \lim_{ n \to 0 }f(x)\text{ esiste } \iff \boxed{a=b} \\ >\end{align}$$ Quindi $f(x)$ è continua soltanto se $a=b$: $$f(x)= \begin{cases} \frac{\sin(\textcolor{orange}{b}x)}{x} &se\ \ x>0 \\ x^{2}+\textcolor{orange}{b} & se\ \ x\leq 0 \\ \end{cases}$$